
【題目】關(guān)于函數(shù)![]() =|cosx|+cos|2x|有下列四個(gè)結(jié)論:①
=|cosx|+cos|2x|有下列四個(gè)結(jié)論:①![]() 是偶函數(shù);②π是
是偶函數(shù);②π是![]() 的最小正周期;③
的最小正周期;③![]() 在[
在[![]() π,
π,![]() π]上單調(diào)遞增;④
π]上單調(diào)遞增;④![]() 的值域?yàn)?/span>[﹣2,2].上述結(jié)論中,正確的個(gè)數(shù)為( )
的值域?yàn)?/span>[﹣2,2].上述結(jié)論中,正確的個(gè)數(shù)為( )
A.1B.2C.3D.4
【答案】B
【解析】
由二倍角的余弦公式和余弦函數(shù)的性質(zhì),化簡![]() ,由
,由![]() ,可判斷①;可令
,可判斷①;可令![]() ,可得
,可得![]() ,由函數(shù)的周期性可判斷②;由
,由函數(shù)的周期性可判斷②;由![]() 的單調(diào)性,結(jié)合復(fù)合函數(shù)的單調(diào)性可判斷③;由二次函數(shù)的單調(diào)性可判斷④.
的單調(diào)性,結(jié)合復(fù)合函數(shù)的單調(diào)性可判斷③;由二次函數(shù)的單調(diào)性可判斷④.
解:f(x)=|cosx|+cos|2x|=|cosx|+2cos2|x|﹣1,
由cos|x|=cosx,可得![]() =|cosx|+2cos2x﹣1=2|cosx|2+|cosx|﹣1,
=|cosx|+2cos2x﹣1=2|cosx|2+|cosx|﹣1,
由![]() =
=![]() ,則
,則![]() 為偶函數(shù),故①正確;
為偶函數(shù),故①正確;
可令t=|cosx|,可得![]() ,
,
由y=|cosx|的最小正周期π,可得![]() 的最小正周期為π,故②正確;
的最小正周期為π,故②正確;
由y=cosx在[﹣![]() ,0]遞增,在[0,
,0]遞增,在[0,![]() ]遞減,可得f(x)在[
]遞減,可得f(x)在[![]() ,π]遞增,在[π,
,π]遞增,在[π,![]() ]遞減,故③錯(cuò)誤;
]遞減,故③錯(cuò)誤;
由t∈[0,1],![]() ,可得
,可得![]() 在[0,1]遞增,則
在[0,1]遞增,則![]() 的值域?yàn)?/span>[﹣1,2],故④錯(cuò)誤.
的值域?yàn)?/span>[﹣1,2],故④錯(cuò)誤.
故選:B.


 培優(yōu)好卷單元加期末卷系列答案
培優(yōu)好卷單元加期末卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為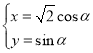 (
(![]() 為參數(shù)).在以
為參數(shù)).在以![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸的極坐標(biāo)系中,直線
軸正半軸為極軸的極坐標(biāo)系中,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)點(diǎn)![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足任意
滿足任意![]() 都有
都有![]() ,且
,且![]() 時(shí),
時(shí),![]() ,則
,則![]() ,
,![]() ,
,![]() 的大小關(guān)系是( )
的大小關(guān)系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某機(jī)構(gòu)組織的家庭教育活動上有一個(gè)游戲,每次由一個(gè)小孩與其一位家長參與,測試家長對小孩飲食習(xí)慣的了解程度.在每一輪游戲中,主持人給出A,B,C,D四種食物,要求小孩根據(jù)自己的喜愛程度對其排序,然后由家長猜測小孩的排序結(jié)果.設(shè)小孩對四種食物排除的序號依次為xAxBxCxD,家長猜測的序號依次為yAyByCyD,其中xAxBxCxD和yAyByCyD都是1,2,3,4四個(gè)數(shù)字的一種排列.定義隨機(jī)變量X=(xA﹣yA)2+(xB﹣yB)2+(xC﹣yC)2+(xD﹣yD)2,用X來衡量家長對小孩飲食習(xí)慣的了解程度.
(1)若參與游戲的家長對小孩的飲食習(xí)慣完全不了解.
(ⅰ)求他們在一輪游戲中,對四種食物排出的序號完全不同的概率;
(ⅱ)求X的分布列(簡要說明方法,不用寫出詳細(xì)計(jì)算過程);
(2)若有一組小孩和家長進(jìn)行來三輪游戲,三輪的結(jié)果都滿足X<4,請判斷這位家長對小孩飲食習(xí)慣是否了解,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
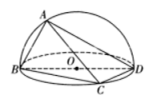
【題目】如圖,已知![]() 是圓
是圓![]() 的直徑,
的直徑,![]() ,
,![]() 在圓上且分別在
在圓上且分別在![]() 的兩側(cè),其中
的兩側(cè),其中![]() ,
,![]() .現(xiàn)將其沿
.現(xiàn)將其沿![]() 折起使得二面角
折起使得二面角![]() 為直二面角,則下列說法不正確的是( )
為直二面角,則下列說法不正確的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一個(gè)球面上
在同一個(gè)球面上
B.當(dāng)![]() 時(shí),三棱錐
時(shí),三棱錐![]() 的體積為
的體積為![]()
C.![]() 與
與![]() 是異面直線且不垂直
是異面直線且不垂直
D.存在一個(gè)位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() 的左焦點(diǎn)為
的左焦點(diǎn)為![]() ,離心率為
,離心率為![]() ,
,![]() 為圓
為圓![]() 的圓心.
的圓心.
(1)求橢圓的方程;
(2)已知過橢圓右焦點(diǎn)![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點(diǎn),過
兩點(diǎn),過![]() 且與
且與![]() 垂直的直線
垂直的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(diǎn),求四邊形
兩點(diǎn),求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是矩形,沿對角線
是矩形,沿對角線![]() 將
將![]() 折起,使得點(diǎn)
折起,使得點(diǎn)![]() 在平面
在平面![]() 上的射影恰好落在邊
上的射影恰好落在邊![]() 上.
上.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)當(dāng)![]() 時(shí),求二面角
時(shí),求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com