
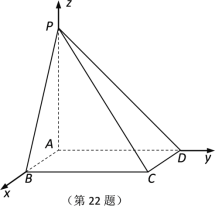
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若點M,N分別在AB,PC上,且![]() 平面
平面![]() ,試確定點M,N的位置.
,試確定點M,N的位置.
【答案】(1)![]() ;(2)M為AB的中點,N為PC的中點
;(2)M為AB的中點,N為PC的中點
【解析】
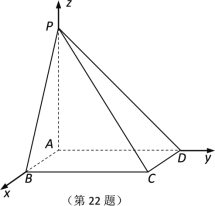
(1)由題意知,AB,AD,AP兩兩垂直.以![]() 為正交基底,建立空間直角坐標系
為正交基底,建立空間直角坐標系![]() ,求平面PCD的一個法向量為
,求平面PCD的一個法向量為![]() ,由空間向量的線面角公式求解即可;(2)設
,由空間向量的線面角公式求解即可;(2)設![]()
![]() ,利用
,利用![]() 平面PCD,所以
平面PCD,所以![]() ∥
∥![]() ,得到
,得到![]() 的方程,求解即可確定M,N的位置
的方程,求解即可確定M,N的位置
(1)由題意知,AB,AD,AP兩兩垂直.
以![]() 為正交基底,建立如圖所示的空間
為正交基底,建立如圖所示的空間
直角坐標系![]() ,則
,則![]()
從而![]()
設平面PCD的法向量![]()
則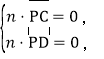 即
即![]()
不妨取![]() 則
則![]() .
.
所以平面PCD的一個法向量為![]() .
.
設直線PB與平面PCD所成角為![]() 所以
所以
即直線PB與平面PCD所成角的正弦值為![]() .
.
(2)設![]() 則
則![]()
設![]() 則
則![]() 而
而![]()
所以![]() .由(1)知,平面PCD的一個法向量為
.由(1)知,平面PCD的一個法向量為![]() ,因為
,因為![]() 平面PCD,所以
平面PCD,所以![]() ∥
∥![]() .
.
所以![]() 解得,
解得,![]() .
.
所以M為AB的中點,N為PC的中點.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )

A. 甲的極差是29 B. 甲的中位數是24
C. 甲罰球命中率比乙高 D. 乙的眾數是21
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(2)設函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,若函數
,若函數![]() 是
是![]() 上的單調增函數,求
上的單調增函數,求![]() 的值;
的值;
(3)是否存在一條直線與函數![]() 的圖象相切于兩個不同的點?并說明理由.
的圖象相切于兩個不同的點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術》中,將底面為直角三角形且側棱垂直于底面的三棱柱稱之為塹堵;將底面為矩形且一側棱垂直于底面的四棱錐稱之為陽馬;將四個面均為直角三角形的四面體稱之為鱉臑[biē nào].某學校科學小組為了節約材料,擬依托校園內垂直的兩面墻和地面搭建一個塹堵形的封閉的實驗室![]() ,
,![]() 是邊長為2的正方形.
是邊長為2的正方形.


(1)若![]() 是等腰三角形,在圖2的網格中(每個小方格都是邊長為1的正方形)畫出塹堵的三視圖;
是等腰三角形,在圖2的網格中(每個小方格都是邊長為1的正方形)畫出塹堵的三視圖;
(2)若![]() ,
,![]() 在
在![]() 上,證明:
上,證明:![]() ,并回答四面體
,并回答四面體![]() 是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,請說明理由;
是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,請說明理由;
(3)當陽馬![]() 的體積最大時,求點
的體積最大時,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
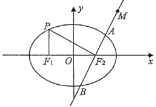
【題目】如圖,在平面直角坐標系xOy中,![]() ,
,![]() 分別是橢圓
分別是橢圓![]() 的左,右焦點,點P是橢圓E上一點,滿足
的左,右焦點,點P是橢圓E上一點,滿足![]() 軸,
軸,![]() .
.
(1)求橢圓E的離心率;
(2)過點![]() 的直線l與橢圓E交于兩點A,B,若在橢圓B上存在點Q,使得四邊形OAQB為平行四邊形,求直線l的斜率.
的直線l與橢圓E交于兩點A,B,若在橢圓B上存在點Q,使得四邊形OAQB為平行四邊形,求直線l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,棱錐P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
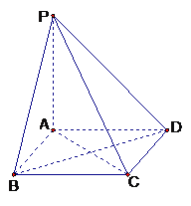
(1)求證:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某區選派7名隊員代表本區參加全市青少年圍棋錦標賽,其中3名來自A學校且1名為女棋手,另外4名來自B學校且2名為女棋手![]() 從這7名隊員中隨機選派4名隊員參加第一階段的比賽
從這7名隊員中隨機選派4名隊員參加第一階段的比賽
![]() 求在參加第一階段比賽的隊員中,恰有1名女棋手的概率;
求在參加第一階段比賽的隊員中,恰有1名女棋手的概率;
![]() Ⅱ
Ⅱ![]() 設X為選出的4名隊員中A、B兩校人數之差的絕對值,求隨機變量X的分布列和數學期望
設X為選出的4名隊員中A、B兩校人數之差的絕對值,求隨機變量X的分布列和數學期望
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com