
【題目】某高校在![]() 年的自主招生考試成績(jī)中隨機(jī)抽取
年的自主招生考試成績(jī)中隨機(jī)抽取![]() 名學(xué)生的筆試成績(jī),按成績(jī)分組:第
名學(xué)生的筆試成績(jī),按成績(jī)分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() 得到的頻率分布直方圖如圖所示
得到的頻率分布直方圖如圖所示
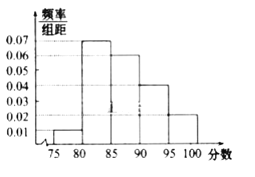
![]() 分別求第
分別求第![]() 組的頻率;
組的頻率;
![]() 若該校決定在第
若該校決定在第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名學(xué)生進(jìn)入第二輪面試,
名學(xué)生進(jìn)入第二輪面試,
![]() 已知學(xué)生甲和學(xué)生乙的成績(jī)均在第
已知學(xué)生甲和學(xué)生乙的成績(jī)均在第![]() 組,求學(xué)生甲和學(xué)生乙同時(shí)進(jìn)入第二輪面試的概率;
組,求學(xué)生甲和學(xué)生乙同時(shí)進(jìn)入第二輪面試的概率;
![]() 根據(jù)直方圖試估計(jì)這
根據(jù)直方圖試估計(jì)這![]() 名學(xué)生成績(jī)的平均分.(同一組中的數(shù)據(jù)用改組區(qū)間的中間值代表)
名學(xué)生成績(jī)的平均分.(同一組中的數(shù)據(jù)用改組區(qū)間的中間值代表)
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根據(jù)頻率分布直方圖的性質(zhì),根據(jù)所給的頻率分布直方圖中小矩形的長(zhǎng)和寬,求出矩形的面積,即這組數(shù)據(jù)的頻率.
(2)①先求得試驗(yàn)發(fā)生包含的事件數(shù)是![]() ,再求得滿足條件的事件數(shù)是
,再求得滿足條件的事件數(shù)是![]() ,根據(jù)等可能事件的概率公式,得到結(jié)果.
,根據(jù)等可能事件的概率公式,得到結(jié)果.
②由頻率分布直方圖的平均數(shù)公式直接計(jì)算即可.
(1)第3組的頻率為 ![]() ;第4組的頻率為
;第4組的頻率為 ![]() ;
;
第5組的頻率為 ![]() .
.
(2)按分層抽樣的方法在第3、4、5組中分別抽取3人、2人、1人.
①第3組共有![]() ,設(shè)“學(xué)生甲和學(xué)生乙同時(shí)進(jìn)入第二輪面試”為事件
,設(shè)“學(xué)生甲和學(xué)生乙同時(shí)進(jìn)入第二輪面試”為事件![]()
![]() ,
,![]() 學(xué)生甲和學(xué)生乙同時(shí)進(jìn)入第二輪面試的概率為
學(xué)生甲和學(xué)生乙同時(shí)進(jìn)入第二輪面試的概率為![]() .
.
②![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列命題:
![]() 用反證法證明命題“設(shè)a,b,c為實(shí)數(shù),且
用反證法證明命題“設(shè)a,b,c為實(shí)數(shù),且![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ”時(shí),要給出的假設(shè)是:a,b,c都不是正數(shù);
”時(shí),要給出的假設(shè)是:a,b,c都不是正數(shù);
![]() 若函數(shù)
若函數(shù)![]() 在
在![]() 處取得極大值,則
處取得極大值,則![]() 或
或![]() ;
;
![]() 用數(shù)學(xué)歸納法證明
用數(shù)學(xué)歸納法證明![]() ,在驗(yàn)證
,在驗(yàn)證![]() 成立時(shí),不等式的左邊是
成立時(shí),不等式的左邊是![]() ;
;
![]() 數(shù)列
數(shù)列![]() 的前n項(xiàng)和
的前n項(xiàng)和![]() ,則
,則![]() 是數(shù)列
是數(shù)列![]() 為等比數(shù)列的充要條件;
為等比數(shù)列的充要條件;
上述命題中,所有正確命題的序號(hào)為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() .
.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() (其中
(其中![]() 為自然對(duì)數(shù)的底數(shù)),且
為自然對(duì)數(shù)的底數(shù)),且![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】即將于![]() 年夏季畢業(yè)的某大學(xué)生準(zhǔn)備到貴州非私營(yíng)單位求職,為了了解工資待遇情況,他在貴州省統(tǒng)計(jì)局的官網(wǎng)上,查詢到
年夏季畢業(yè)的某大學(xué)生準(zhǔn)備到貴州非私營(yíng)單位求職,為了了解工資待遇情況,他在貴州省統(tǒng)計(jì)局的官網(wǎng)上,查詢到![]() 年到
年到![]() 年非私營(yíng)單位在崗職工的年平均工資近似值(單位:萬元),如下表:
年非私營(yíng)單位在崗職工的年平均工資近似值(單位:萬元),如下表:
年份 |
|
|
|
|
|
|
|
|
|
|
序號(hào) |
|
|
|
|
|
|
|
|
|
|
年平均工資 |
|
|
|
|
|
|
|
|
|
|
(1)請(qǐng)根據(jù)上表的數(shù)據(jù),利用線性回歸模型擬合思想,求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() (
(![]() ,
,![]() 的計(jì)算結(jié)果根據(jù)四舍五入精確到小數(shù)點(diǎn)后第二位);
的計(jì)算結(jié)果根據(jù)四舍五入精確到小數(shù)點(diǎn)后第二位);
(2)如果畢業(yè)生對(duì)年平均工資的期望值為8.5萬元,請(qǐng)利用(1)的結(jié)論,預(yù)測(cè)![]() 年的非私營(yíng)單位在崗職工的年平均工資(單位:萬元。計(jì)算結(jié)果根據(jù)四舍五入精確到小數(shù)點(diǎn)后第二位),并判斷
年的非私營(yíng)單位在崗職工的年平均工資(單位:萬元。計(jì)算結(jié)果根據(jù)四舍五入精確到小數(shù)點(diǎn)后第二位),并判斷![]() 年平均工資能否達(dá)到他的期望.
年平均工資能否達(dá)到他的期望.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附:對(duì)于一組具有線性相關(guān)的數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其回歸直線![]() 的斜率和截距的最小二乘法估計(jì)分別為
的斜率和截距的最小二乘法估計(jì)分別為

 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若對(duì)于函數(shù)f(x)=ln(x+1)+x2圖象上任意一點(diǎn)處的切線l1,在函數(shù)g(x)![]() asin
asin![]() cos
cos![]() x圖象上總存在一條切線l2,使得l1⊥l2,則實(shí)數(shù)a的取值范圍為( )
x圖象上總存在一條切線l2,使得l1⊥l2,則實(shí)數(shù)a的取值范圍為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年12月1日,貴陽市地鐵一號(hào)線全線開通,在一定程度上緩解了出行的擁堵狀況.為了了解市民對(duì)地鐵一號(hào)線開通的關(guān)注情況,某調(diào)查機(jī)構(gòu)在地鐵開通后的某兩天抽取了部分乘坐地鐵的市民作為樣本,分析其年齡和性別結(jié)構(gòu),并制作出如下等高條形圖:
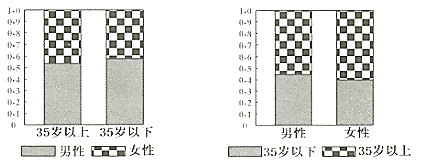
根據(jù)圖中(![]() 歲以上含
歲以上含![]() 歲)的信息,下列結(jié)論中不一定正確的是( )
歲)的信息,下列結(jié)論中不一定正確的是( )
A. 樣本中男性比女性更關(guān)注地鐵一號(hào)線全線開通
B. 樣本中多數(shù)女性是![]() 歲以上
歲以上
C. ![]() 歲以下的男性人數(shù)比
歲以下的男性人數(shù)比![]() 歲以上的女性人數(shù)多
歲以上的女性人數(shù)多
D. 樣本中![]() 歲以上的人對(duì)地鐵一號(hào)線的開通關(guān)注度更高
歲以上的人對(duì)地鐵一號(hào)線的開通關(guān)注度更高
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一次抽獎(jiǎng)活動(dòng)中,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6人獲得抽獎(jiǎng)機(jī)會(huì),抽獎(jiǎng)規(guī)則如下:若獲一等獎(jiǎng)后不再參加抽獎(jiǎng),獲得二等獎(jiǎng)的仍參加三等獎(jiǎng)抽獎(jiǎng).現(xiàn)在主辦方先從6人中隨機(jī)抽取2人均獲一等獎(jiǎng),再從余下的4人中隨機(jī)抽取1人獲二等獎(jiǎng),最后還從這4人中隨機(jī)抽取1人獲三等獎(jiǎng).
共6人獲得抽獎(jiǎng)機(jī)會(huì),抽獎(jiǎng)規(guī)則如下:若獲一等獎(jiǎng)后不再參加抽獎(jiǎng),獲得二等獎(jiǎng)的仍參加三等獎(jiǎng)抽獎(jiǎng).現(xiàn)在主辦方先從6人中隨機(jī)抽取2人均獲一等獎(jiǎng),再從余下的4人中隨機(jī)抽取1人獲二等獎(jiǎng),最后還從這4人中隨機(jī)抽取1人獲三等獎(jiǎng).
(1)求![]() 能獲一等獎(jiǎng)的概率;
能獲一等獎(jiǎng)的概率;
(2)若![]() ,
,![]() 已獲一等獎(jiǎng),求
已獲一等獎(jiǎng),求![]() 能獲獎(jiǎng)的概率.
能獲獎(jiǎng)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在線段
在線段![]() 上運(yùn)動(dòng),且
上運(yùn)動(dòng),且![]() .
.
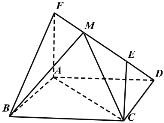
(1)當(dāng)![]() 時(shí),求異面直線
時(shí),求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(2)設(shè)平面![]() 與平面
與平面![]() 所成二面角的大小為
所成二面角的大小為![]() (
(![]() ),求
),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com