
【題目】在平面直角坐標系中,設點![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的較大數)為
表示a、b中的較大數)為![]() 、
、![]() 兩點的“切比雪夫距離”.
兩點的“切比雪夫距離”.
(1)若![]() ,Q為直線
,Q為直線![]() 上動點,求P、Q兩點“切比雪夫距離”的最小值;
上動點,求P、Q兩點“切比雪夫距離”的最小值;
(2)定點![]() ,動點
,動點![]() 滿足
滿足![]()
![]() ,請求出P點所在的曲線所圍成圖形的面積.
,請求出P點所在的曲線所圍成圖形的面積.
科目:高中數學 來源: 題型:
【題目】有下列幾個命題:①“若p,則q”的否命題是“若![]() ,則
,則![]() ”;②p是q的必要條件,r是q的充分不必要條件,則p是r的必要不充分條件;③若“
”;②p是q的必要條件,r是q的充分不必要條件,則p是r的必要不充分條件;③若“![]() ”為真命題,則命題p,q中至多有一個為真命題;④過點
”為真命題,則命題p,q中至多有一個為真命題;④過點![]() 的直線和圓
的直線和圓![]() 相切的充要條件是直線斜率為
相切的充要條件是直線斜率為![]() .其中為真命題的有( )
.其中為真命題的有( )
A.①②B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】生活中人們常用“通五經貫六藝”形容一個人才識技藝過人,這里的“六藝”其實源于中國周朝的貴族教育體系,具體包括“禮、樂、射、御、書、數”.為弘揚中國傳統文化,某校在周末學生業余興趣活動中開展了“六藝”知識講座,每藝安排一節,連排六節,則滿足“數”必須排在前兩節,“禮”和“樂”必須分開安排的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,點
,點![]() 是橢圓上任意一點,
是橢圓上任意一點,![]() 的最小值為
的最小值為![]() ,且該橢圓的離心率為
,且該橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 是橢圓
是橢圓![]() 上不同的兩點,且
上不同的兩點,且![]() ,若
,若![]() ,試問直線
,試問直線![]() 是否經過一個定點?若經過定點,求出該定點的坐標;若不經過定點,請說明理由.
是否經過一個定點?若經過定點,求出該定點的坐標;若不經過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下面四個命題:
①“若![]() ,則
,則![]() 或
或![]() ”的逆否命題為“若
”的逆否命題為“若![]() 且
且![]() ,則
,則![]() ”
”
②“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
③命題![]() 存在
存在![]() ,使得
,使得![]() ,則
,則![]() :任意
:任意![]() ,都有
,都有![]()
④若![]() 且
且![]() 為假命題,則
為假命題,則![]() 均為假命題,其中真命題個數為( )
均為假命題,其中真命題個數為( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過隨機詢問50名性別不同的大學生是否愛好某項運動,得到如下的列聯表,由![]() 得
得![]()
參照附表,得到的正確結論是
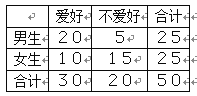

A. 有99.5%以上的把握認為“愛好該項運動與性別有關”
B. 有99.5%以上的把握認為“愛好該項運動與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() ABC中,角A,B,C所對的邊分別為a,b,c,且asinAcosC+csinAcosA=
ABC中,角A,B,C所對的邊分別為a,b,c,且asinAcosC+csinAcosA=![]() c.
c.
(1)若c=1,sinC=![]() ,求
,求![]() ABC的面積S;
ABC的面積S;
(2)若D是AC的中點,且cosB=![]() ,BD=
,BD=![]() ,求
,求![]() ABC的三邊長.
ABC的三邊長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com