
【題目】設{an}是等差數列,{bn}是各項都為正數的等比數列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通項公式;
(2)求數列 ![]() 的前n項和Sn .
的前n項和Sn .
【答案】
(1)解:設{an}的公差為d,{bn}的公比為q,則依題意有q>0且 ![]()
解得d=2,q=2.
所以an=1+(n﹣1)d=2n﹣1,bn=qn﹣1=2n﹣1.
(2)解: ![]() ,
,
![]() ,①
,①
![]() Sn=
Sn= ![]()
![]() ,②
,②
①﹣②得 ![]() Sn=1+2(
Sn=1+2( ![]() +
+ ![]() +…+
+…+ ![]() )﹣
)﹣ ![]() ,
,
則 ![]() =
= ![]() =
= 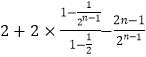 =
= ![]() .
.
【解析】(1)設{an}的公差為d,{bn}的公比為q,根據等比數列和等差數列的通項公式,聯立方程求得d和q,進而可得{an}、{bn}的通項公式.(2)數列 ![]() 的通項公式由等差和等比數列構成,進而可用錯位相減法求得前n項和Sn .
的通項公式由等差和等比數列構成,進而可用錯位相減法求得前n項和Sn .
【考點精析】掌握等差數列的通項公式(及其變式)和等比數列的通項公式(及其變式)是解答本題的根本,需要知道通項公式:![]() 或
或![]() ;通項公式:
;通項公式:![]() .
.


科目:高中數學 來源: 題型:
【題目】某市共有初中學生270000人,其中初一年級,初二年級,初三年級學生人數分別為99000,90000,81000,為了解該市學生參加“開放性科學實驗活動”的意向,現采用分層抽樣的方法從中抽取一個容量為3000的樣本,那么應該抽取初三年級的人數為( )
A.800
B.900
C.1000
D.1100
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與
與![]() 、
、![]() 軸交于
軸交于![]() 、
、![]() 兩點.
兩點.
(Ⅰ)若點![]() 、
、![]() 分別是雙曲線
分別是雙曲線![]() 的虛軸、實軸的一個端點,試在平面上找兩點
的虛軸、實軸的一個端點,試在平面上找兩點![]() 、
、![]() ,使得雙曲線
,使得雙曲線![]() 上任意一點到
上任意一點到![]() 、
、![]() 這兩點距離差的絕對值是定值.
這兩點距離差的絕對值是定值.
(Ⅱ)若以原點![]() 為圓心的圓
為圓心的圓![]() 截直線
截直線![]() 所得弦長是
所得弦長是![]() ,求圓
,求圓![]() 的方程以及這條弦的中點.
的方程以及這條弦的中點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,直線
,直線![]() (其中
(其中![]() )與曲線
)與曲線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
(Ⅰ)若![]() ,試判斷曲線
,試判斷曲線![]() 的形狀.
的形狀.
(Ⅱ)若![]() ,以線段
,以線段![]() 、
、![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,其中頂點
,其中頂點![]() 在曲線
在曲線![]() 上,
上, ![]() 為坐標原點,求
為坐標原點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角三角形中,邊a、b是方程x2﹣2 ![]() x+2=0的兩根,角A、B滿足:2sin(A+B)﹣
x+2=0的兩根,角A、B滿足:2sin(A+B)﹣ ![]() =0,求角C的度數,邊c的長度及△ABC的面積.
=0,求角C的度數,邊c的長度及△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且滿足Sn=2an﹣2.若數列{bn}滿足bn=10﹣log2an , 則是數列{bn}的前n項和取最大值時n的值為( )
A.8
B.10
C.8或9
D.9或10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品店為了了解氣溫對銷售量的影響,隨機記錄了該店1月份中5天的日銷售量![]() (單位:千克)與該地當日最低氣溫
(單位:千克)與該地當日最低氣溫![]() (單位:
(單位: ![]() )的數據,如下表:
)的數據,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 與
與![]() 的回歸方程
的回歸方程![]() ;
;
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;若該地1月份某天的最低氣溫為
之間是正相關還是負相關;若該地1月份某天的最低氣溫為![]() ,請用所求回歸方程預測該店當日的銷售量;
,請用所求回歸方程預測該店當日的銷售量;
(3)設該地1月份的日最低氣溫![]() ~
~![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
, ![]() 近似為樣本方差
近似為樣本方差![]() ,求
,求![]() .
.
附:①回歸方程![]() 中,
中, 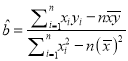 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com