
【題目】已知數列![]() 是公差不為0的等差數列,
是公差不為0的等差數列, ![]() 是等比數列,且
是等比數列,且![]()
![]()
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前n項的和
的前n項的和![]() .
.
【答案】(1)![]() ;(2)
;(2)
【解析】試題分析:(1)設等差數列![]() 的公差為
的公差為![]() ,等比數列
,等比數列![]() 的公比為
的公比為![]() ,由
,由![]() ,可得
,可得![]() ,解出即可得出數列
,解出即可得出數列![]() 和
和![]() 的通項公式;(2)
的通項公式;(2)![]() ,設數列
,設數列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() ,
, ![]() ,當
,當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,進而可得結果.
,進而可得結果.
試題解析:(1)設等差數列{an}的公差為d≠0,等比數列{bn}的公比為q,∵b1=a1=3,b2=a3,b3=a9.∴![]() ,解得d=3,q=3.∴an=3+3(n﹣1)=3n,bn=3n.
,解得d=3,q=3.∴an=3+3(n﹣1)=3n,bn=3n.
(2)![]() =5n﹣32,
=5n﹣32,
設數列{cn}的前n項和為Tn,則Tn=![]() =
=![]() ,令cn≥0,解得n≥7,∴|cn|=
,令cn≥0,解得n≥7,∴|cn|=![]() ,∴當n≤6時,Sn=﹣(a1+a2+…+an)=﹣Tn=
,∴當n≤6時,Sn=﹣(a1+a2+…+an)=﹣Tn=![]() ,當n≥7時,Sn=﹣T6+a7+a8+…+an=Tn﹣2T6=
,當n≥7時,Sn=﹣T6+a7+a8+…+an=Tn﹣2T6=![]() +174,∴數列{|cn|}的前n項的和Sn=
+174,∴數列{|cn|}的前n項的和Sn=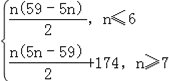 .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知2件次品和3件正品混放在一起,現需要通過檢測將其區分,每次隨機檢測一件產品,檢測后不放回,直到檢測出2件次品或者檢測出3件正品時檢測結束.
(Ⅰ)求第一次檢測出的是次品且第二次檢測出的是正品的概率;
(Ⅱ)已知每檢測一件產品需要費用100元,設![]() 表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求
表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為常數.
為常數.
(1)當![]() ,且
,且![]() 時,判斷函數
時,判斷函數![]() 是否存在極值,若存在,求出極值點;若不存在,說明理由;
是否存在極值,若存在,求出極值點;若不存在,說明理由;
(2)若![]() ,對任意的正整數
,對任意的正整數![]() ,當
,當![]() 時,求證:
時,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O的方程為x2+y2=4,P是圓O上的一個動點,若線段OP的垂直平分線總是被平面區域|x|+|y|≥a覆蓋,則實數a的取值范圍是( )
A.0≤a≤2
B.![]()
C.0≤a≤1
D.a≤1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班學生進行了三次數學測試,第一次有8名學生得滿分,第二次有10名學生得滿分,第三次有12名學生得滿分,已知前兩次均為滿分的學生有5名,三次測試中至少有一次得滿分的學生有15名,若后兩次均為滿分的學生至少有![]() 名,則
名,則![]() 的值為( )
的值為( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列函數中,奇函數的個數為( ) ①y=x2sinx ②y=sinx , x∈ ![]() ③y=xcosx , x∈
③y=xcosx , x∈ ![]() ④y=tanx .
④y=tanx .
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+x2﹣ax(a∈R)
(1)a=3時,求函數f(x)的單調區間;
(2)若f(x)≤2x2恒成立,求實數a的取值范圍;
(3)求證;lnn> ![]() +
+ ![]() +1
+1 ![]() +…+
+…+ ![]() (n∈N+)且n≥2.
(n∈N+)且n≥2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com