
【題目】已知函數f(x)=lnx+x2﹣ax(a∈R)
(1)a=3時,求函數f(x)的單調區間;
(2)若f(x)≤2x2恒成立,求實數a的取值范圍;
(3)求證;lnn> ![]() +
+ ![]() +1
+1 ![]() +…+
+…+ ![]() (n∈N+)且n≥2.
(n∈N+)且n≥2.
【答案】
(1)解:a=3時,f(x)=lnx+x2﹣3x,(x>0),
f′(x)= ![]() +2x﹣3=
+2x﹣3= ![]() ,
,
△=32﹣8=1>0,由f′(x)=0,解得x1= ![]() ,x2=1,
,x2=1,
當x∈(0, ![]() )∪(1,+∞)時,f′(x)>0,當x∈(
)∪(1,+∞)時,f′(x)>0,當x∈( ![]() )時,f′(x)<0,
)時,f′(x)<0,
則函數f(x)在(0, ![]() ),(1,+∞)上單調遞增,在(
),(1,+∞)上單調遞增,在( ![]() ,1)上單調遞減
,1)上單調遞減
(2)解:f(x)≤2x2,化為:lnx﹣x2﹣ax≤0,
∴a≥ ![]() ﹣x,令g(x)=
﹣x,令g(x)= ![]() ,
,
g′(x)= ![]() ,
,
令h(x)=1﹣lnx﹣x2,可知:函數h(x)在(0,+∞)上單調遞減.
而h(1)=0=g′(1).
∴x>1時,g′(x)<0,函數g(x)單調遞減;
0<x<1時,g′(x)>0,函數g(x)單調遞增.
∴函數g(x)在x=1時取得極大值即最大值,g(1)=﹣1.
∴實數a的取值范圍是a≥﹣1
(3)證明:令t(x)=lnx﹣ ![]() ,
,
則t′(x)= ![]() >0,
>0,
∴t(x)在(0,+∞)上單調遞增,
當x>1時,t(x)>t(1),即lnx﹣ ![]() >0,∴lnx>
>0,∴lnx> ![]() ,
,
令x=1+ ![]() ,則ln(1+
,則ln(1+ ![]() )>
)> 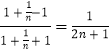 ,
,
故ln(1+1)> ![]() ,ln(1+
,ln(1+ ![]() )>
)> ![]() ,…,ln(1+
,…,ln(1+ ![]() )>
)> ![]() .
.
累加得:ln(n+1)> ![]() ,
,
取n=n﹣1,得lnn> ![]() (n≥2)
(n≥2)
【解析】(1)把a=3代入函數解析式,求導后求得導函數零點,由導函數零點對定義域分段,求出各區間段內導函數的符號,從而求得原函數的單調區間;(2)把f(x)≤2x2化為:lnx﹣x2﹣ax≤0,得到a≥ ![]() ﹣x,令g(x)=
﹣x,令g(x)= ![]() ,利用導數求其最大值可得實數a的取值范圍;(3)令t(x)=lnx﹣
,利用導數求其最大值可得實數a的取值范圍;(3)令t(x)=lnx﹣ ![]() ,由導數可得t(x)在(0,+∞)上單調遞增,得到x>1時,lnx>
,由導數可得t(x)在(0,+∞)上單調遞增,得到x>1時,lnx> ![]() ,令x=1+
,令x=1+ ![]() ,可得ln(1+
,可得ln(1+ ![]() )>
)> 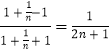 ,累加可得ln(n+1)>
,累加可得ln(n+1)> ![]() ,取n=n﹣1得答案.
,取n=n﹣1得答案.
【考點精析】根據題目的已知條件,利用利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識可以得到問題的答案,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在中學生綜合素質評價某個維度的測評中,分“優秀、合格、尚待改進”三個等級進行學生互評,某校高二年級有男生500人,女生400人,為了了解性別對維度測評結果的影響,采用分層抽樣方法從高二年級抽取了45名學生的測評結果,并作出頻率統計表如表: 表一:男生測評結果統計
等級 | 優秀 | 合格 | 尚待改進 |
頻數 | 15 | x | 5 |
表二:女生測評結果統計
等級 | 優秀 | 合格 | 尚待改進 |
頻數 | 15 | 3 | y |
參考數據:
P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(參考公式: ![]() ,其中n=a+b+c+d).
,其中n=a+b+c+d).
(1)計算x,y的值;
(2)由表一表二中統計數據完成2×2列聯表,并判斷是否有90%的把握認為“測評結果優秀與性別有關”.
男生 | 女生 | 總計 | |
優秀 | |||
非優秀 | |||
總計 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com