【題目】某條公共汽車線路收支差額
與乘客量
的函數關系如下圖所示（收支差額＝車票收入－支出費用），由于目前本條線路虧損，公司有關人員提出了兩條建議：建議（1）不改變車票價格，減少支出費用；建議（2）不改變支出費用，提高車票價格.下面給出的四個圖形中，實線和虛線分別表示目前和建議后的函數關系，則（ ）
A.①反映建議（2），③反映建議（1）B.①反映建議（1），③反映建議（2）
C.②反映建議（1），④反映建議（2）D.④反映建議（1），②反映建議（2）
科目：高中數學 來源： 題型：
【題目】已知拋物線C：y2=2px過點P（1，1）.過點（0， 
）作直線l與拋物線C交于不同的兩點M，N，過點M作x軸的垂線分別與直線OP，ON交于點A，B，其中O為原點.
（Ⅰ）求拋物線C的方程，并求其焦點坐標和準線方程；
（Ⅱ）求證：A為線段BM的中點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的焦點和上頂點分別為
，定義：
為橢圓
的“特征三角形”，如果兩個橢圓的特征三角形是相似三角形，那么稱這兩個橢圓為“相似橢圓”，且特征三角形的相似比即為相似橢圓的相似比，已知點
是橢圓
的一個焦點，且
上任意一點到它的兩焦點的距離之和為4
（1）若橢圓
與橢圓相似，且與的相似比為2：1，求橢圓的方程.
（2）已知點
是橢圓上的任意一點，若點
是直線
與拋物線
異于原點的交點，證明：點一定在雙曲線
上.
（3）已知直線
，與橢圓相似且短半軸長為
的橢圓為
，是否存在正方形
，（設其面積為
），使得
在直線
上，
在曲線上？若存在，求出函數
的解析式及定義域；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在新中國成立70周年國慶閱兵慶典中，眾多群眾在臉上貼著一顆紅心，以此表達對祖國的熱愛之情，在數學中，有多種方程都可以表示心型曲線，其中有著名的笛卡爾心型曲線，如圖，在直角坐標系中，以原點O為極點，x軸正半軸為極軸建立極坐標系.圖中的曲線就是笛卡爾心型曲線，其極坐標方程為
（
），M為該曲線上的任意一點.
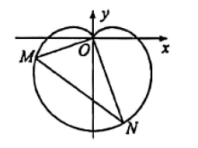
（1）當
時，求M點的極坐標；
（2）將射線OM繞原點O逆時針旋轉
與該曲線相交于點N，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
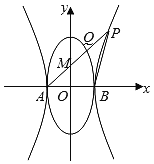
【題目】如圖，橢圓
的左、右頂點分別為A、B，雙曲線
以A、B為頂點，焦距為
，點P是上在第一象限內的動點，直線AP與橢圓相交于另一點Q，線段AQ的中點為M，記直線AP的斜率為
為坐標原點.
(1)求雙曲線的方程；
(2)求點M的縱坐標
的取值范圍；
(3)是否存在定直線
使得直線BP與直線OM關于直線
對稱？若存在，求直線的方程；若不存在,請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
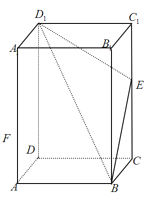
【題目】如圖，已知在長方體
中，
，點
為
上的一個動點，平面
與棱
交于點
，給出下列命題：
①四棱錐
的體積為
；
②存在唯一的點，使截面四邊形
的周長取得最小值
；
③當點不與
，
重合時，在棱
上均存在點
，使得
平面
④存在唯一一點，使得
平面，且
其中正確的命題是_____________（填寫所有正確的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
，圓
，動圓P與圓M外切并且與圓N內切，圓心P的軌跡為曲線C.
（1）求曲線C的方程；
（2）設不經過點
的直線l與曲線C相交于A，B兩點，直線QA與直線QB的斜率均存在且斜率之和為-2，證明：直線l過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
