
���}Ŀ������С�}�M(m��n)��12�֣���֪�c(di��n)![]() �钁�タ(xi��n)
�钁�タ(xi��n)![]() �Ľ��c(di��n)���c(di��n)
�Ľ��c(di��n)���c(di��n)![]() �ڒ��タ(xi��n)
�ڒ��タ(xi��n)![]() �ϣ���
�ϣ���![]() ��
��

���������タ(xi��n)![]() �ķ��̣�
�ķ��̣�
��������֪�c(di��n)![]() �����L(zh��ng)
�����L(zh��ng)![]() �����タ(xi��n)
�����タ(xi��n)![]() ���c(di��n)
���c(di��n)![]() ���C�������c(di��n)
���C�������c(di��n)![]() ��A�����cֱ��(xi��n)
��A�����cֱ��(xi��n)![]() ���еĈA�����cֱ��(xi��n)
���еĈA�����cֱ��(xi��n)![]() ���У�
����
���𰸡�������![]() ��������ԔҊ(ji��n)������
��������ԔҊ(ji��n)������
���������ⷨһ���������ɒ��タ(xi��n)�Ķ��x��![]() ��
��
��?y��n)?/span>![]() ����
����![]() �����
�����![]() ������?hu��)��タ(xi��n)
������?hu��)��タ(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��
��������?y��n)��c(di��n)![]() �ڒ��タ(xi��n)
�ڒ��タ(xi��n)![]()
![]() �ϣ�
�ϣ�
����![]() ���ɒ��タ(xi��n)�Č�(du��)�Q(ch��ng)�ԣ������O(sh��)
���ɒ��タ(xi��n)�Č�(du��)�Q(ch��ng)�ԣ������O(sh��)![]() ��
��
��![]() ��
��![]() �ɵ�ֱ��(xi��n)
�ɵ�ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��
��![]() ����
����![]() ��
��
���![]() ��
��![]() ���Ķ�
���Ķ�![]() ��
��
��![]() ��
��
����![]() ��
��![]() ��
��
����![]() ���Ķ�
���Ķ�![]() ���@�����c(di��n)
���@�����c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() ��
��![]() �ľ��x��ȣ�
�ľ��x��ȣ�
����![]() ��A�����cֱ��(xi��n)
��A�����cֱ��(xi��n)![]() ���еĈA���cֱ��(xi��n)
���еĈA���cֱ��(xi��n)![]() ���У�
����
�ⷨ����������ͬ�ⷨһ��
�������O(sh��)���c(di��n)![]() ��A�����cֱ��(xi��n)
��A�����cֱ��(xi��n)![]() ���еĈA�İ돽��
���еĈA�İ돽��![]() ��
��
��?y��n)��c(di��n)![]() �ڒ��タ(xi��n)
�ڒ��タ(xi��n)![]()
![]() �ϣ�
�ϣ�
����![]() ���ɒ��タ(xi��n)�Č�(du��)�Q(ch��ng)�ԣ������O(sh��)
���ɒ��タ(xi��n)�Č�(du��)�Q(ch��ng)�ԣ������O(sh��)![]() ��
��
��![]() ��
��![]() �ɵ�ֱ��(xi��n)
�ɵ�ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��
��![]() ����
����![]() ��
��
���![]() ��
��![]() ���Ķ�
���Ķ�![]() ��
��
��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��
�Ķ�![]() ��
��
��ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��
�����c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x
�ľ��x![]() ��
��
�@�������c(di��n)![]() ��A�����cֱ��(xi��n)
��A�����cֱ��(xi��n)![]() ���еĈA���cֱ��(xi��n)
���еĈA���cֱ��(xi��n)![]() ���У�
����



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����б������ABC��A1B1C1�У���(c��)��ACC1A1�c��(c��)��CBB1C1�������Σ���ACC1=��CC1B1=60�㣬AC=2�� 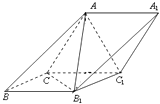
��1�����C��AB1��CC1��
��2���� ![]() ��������C��AB1��A1������ֵ��
��������C��AB1��A1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����
��1����ax��lnx���������(sh��)��(sh��)a��ȡֵ������
��2���C����a��0��x0��R��ʹ�î�(d��ng)x��x0�r(sh��)��ax��lnx�������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���õ�߅�L(zh��ng)��2����������![]() ��
��![]() �S�L��(d��ng), �O(sh��)��c(di��n)
�S�L��(d��ng), �O(sh��)��c(di��n)![]() �Ŀv����(bi��o)�c�M����(bi��o)�ĺ���(sh��)�P(gu��n)ϵʽ��
�Ŀv����(bi��o)�c�M����(bi��o)�ĺ���(sh��)�P(gu��n)ϵʽ��![]() �� �����нY(ji��)Փ:
�� �����нY(ji��)Փ:
�ٺ���(sh��)![]() ��ֵ����
��ֵ����![]() ���ڌ�(du��)�����
���ڌ�(du��)�����![]() ������
������![]() ��
��
�ۺ���(sh��)![]() ��ż����(sh��)���ܺ���(sh��)
��ż����(sh��)���ܺ���(sh��)![]() ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��![]() .
.
�������_�Y(ji��)Փ����̖(h��o)��________. (��(xi��)���������_�Y(ji��)Փ����̖(h��o))
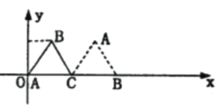
�f(shu��)��:
����������![]() ��
��![]() �S�L��(d��ng)��������
�S�L��(d��ng)��������![]() �S���������
�S���������![]() �Sؓ(f��)����L��(d��ng). ��
�Sؓ(f��)����L��(d��ng). ��![]() �S������L��(d��ng)ָ����������c(di��n)
�S������L��(d��ng)ָ����������c(di��n)![]() ������형r(sh��)����D(zhu��n), ��(d��ng)��c(di��n)
������형r(sh��)����D(zhu��n), ��(d��ng)��c(di��n)![]() ����
����![]() �S�ϕr(sh��), ������c(di��n)
�S�ϕr(sh��), ������c(di��n)![]() ������형r(sh��)����D(zhu��n), ����^�m(x��). �(l��i)�Ƶ�, ��������
������형r(sh��)����D(zhu��n), ����^�m(x��). �(l��i)�Ƶ�, ��������![]() ������
������![]() �Sؓ(f��)����L��(d��ng).
�Sؓ(f��)����L��(d��ng).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)f��x��=|x��4|��g��x��=|2x+1|��
��1���ⲻ��ʽf��x����g��x����
��2����2f��x��+g��x����ax��(du��)����Č�(sh��)��(sh��)x���������a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��
����������(sh��)![]() ��
��![]() ̎���о�(xi��n)���̞�
̎���о�(xi��n)���̞�![]() ����
����![]() ��ֵ��
��ֵ��
����(d��ng)![]() �r(sh��)��������ʽ
�r(sh��)��������ʽ![]() ���������
���������![]() ��ȡֵ������
��ȡֵ������
����(d��ng)![]() �r(sh��)��������
�r(sh��)��������![]() ��
��![]() �Ͽ��Ѓɂ�(g��)���ȵČ�(sh��)���� ��
�Ͽ��Ѓɂ�(g��)���ȵČ�(sh��)���� ��![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����߅�L(zh��ng)����������(sh��)���������У����L(zh��ng)��2009���������c���L(zh��ng)��2012����������һ�N�Ă�(g��)��(sh��)��?�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]()
![]() �錍(sh��)��(sh��)����
�錍(sh��)��(sh��)����![]() ,
,
(I)��![]() �Ľ⣻
�Ľ⣻
(II)��![]() �M(m��n)��
�M(m��n)��![]() �����C����
�����C����![]() ��
��![]() ��
��
(III)�ڣ�2���ėl���£����C�����P(gu��n)ϵʽ![]() ���õ����P(gu��n)��
���õ����P(gu��n)��![]() �ķ���
�ķ���![]() ����
����![]() ��ʹ
��ʹ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij��(chu��ng)�I(y��)�F(tu��n)�(du��)�M���a(ch��n)![]() �ɷN�a(ch��n)Ʒ������(j��)�Ј�(ch��ng)�A(y��)�y(c��)��
�ɷN�a(ch��n)Ʒ������(j��)�Ј�(ch��ng)�A(y��)�y(c��)��![]() �a(ch��n)Ʒ������(r��n)�cͶ�Y�~�����ȣ���D1����
�a(ch��n)Ʒ������(r��n)�cͶ�Y�~�����ȣ���D1����![]() �a(ch��n)Ʒ������(r��n)�cͶ�Y�~�����g(sh��)ƽ����������(��D2).(ע: ����(r��n)�cͶ�Y�~�Ć�λ�����f(w��n)Ԫ)
�a(ch��n)Ʒ������(r��n)�cͶ�Y�~�����g(sh��)ƽ����������(��D2).(ע: ����(r��n)�cͶ�Y�~�Ć�λ�����f(w��n)Ԫ)

��ע������(r��n)�cͶ�Y�~�Ć�λ�����f(w��n)Ԫ��
(1)�քe��![]() �ɷN�a(ch��n)Ʒ������(r��n)
�ɷN�a(ch��n)Ʒ������(r��n)![]() ��
��![]() ��ʾ��Ͷ�Y�~
��ʾ��Ͷ�Y�~![]() �ĺ���(sh��)��
���(sh��)��
(2)ԓ�F(tu��n)�(du��)�ѻI����10 �f(w��n)Ԫ�Y�𣬲�����ȫ��Ͷ��![]() �ɷN�a(ch��n)Ʒ�����a(ch��n)����(w��n):��(d��ng)
�ɷN�a(ch��n)Ʒ�����a(ch��n)����(w��n):��(d��ng)![]() �a(ch��n)Ʒ��Ͷ�Y�~������f(w��n)Ԫ�r(sh��)�����a(ch��n)
�a(ch��n)Ʒ��Ͷ�Y�~������f(w��n)Ԫ�r(sh��)�����a(ch��n)![]() �ɷN�a(ch��n)Ʒ�ܫ@���������(r��n)���������(r��n)�����?
�ɷN�a(ch��n)Ʒ�ܫ@���������(r��n)���������(r��n)�����?
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com