
【題目】為建設美麗鄉村,政府欲將一塊長12百米,寬5百米的矩形空地ABCD建成生態休閑園,園區內有一景觀湖EFG(圖中陰影部分).以AB所在直線為x軸,AB的垂直平分線為y軸,建立平面直角坐標系xOy(如圖所示).景觀湖的邊界曲線符合函數![]() 模型.園區服務中心P在x軸正半軸上,PO=
模型.園區服務中心P在x軸正半軸上,PO=![]() 百米.
百米.

(1)若在點O和景觀湖邊界曲線上一點M之間修建一條休閑長廊OM,求OM的最短長度;
(2)若在線段DE上設置一園區出口Q,試確定Q的位置,使通道直線段PQ最短.
【答案】(1) ![]() 的最小值為
的最小值為![]() 百米.
百米.
(2) 當點![]() 在線段
在線段![]() 上且距離
上且距離![]() 軸
軸![]() 百米,通道PQ最短.
百米,通道PQ最短.
【解析】
(1)設![]() ,
,![]() ,求出
,求出![]()
![]() ,再利用基本不等式求OM的最短長度.(2) 當直線
,再利用基本不等式求OM的最短長度.(2) 當直線![]() 與邊界曲線相切時,
與邊界曲線相切時,![]() 最短.設切點為
最短.設切點為![]() ,求出切點為
,求出切點為![]() ,切線方程為
,切線方程為![]() ,令
,令![]() ,得
,得![]() ,即點
,即點![]() 在線段
在線段![]() 上且距離
上且距離![]() 軸
軸![]() 百米.
百米.
(1)設![]() ,
,![]() ,
,
則![]()
![]()
![]() ,
,
當且僅當![]() ,即
,即![]() 時取等號.
時取等號.
所以![]() 的最小值為
的最小值為![]() 百米.
百米.
(2)當直線![]() 與邊界曲線相切時,
與邊界曲線相切時,![]() 最短.
最短.
設切點為![]() ,由
,由![]() 得
得![]() ,
,
所以切線的方程為![]() .
.
因為![]() 在
在![]() 軸正半軸上,且PO=
軸正半軸上,且PO=![]() ,所以
,所以![]() 點坐標為
點坐標為![]() .
.
因為切線過點![]() ,所以
,所以![]() ,
,
整理得![]() ,解得
,解得![]() ,或
,或![]() .
.
因為![]() ,所以
,所以![]() ,此時切點為
,此時切點為![]() ,切線方程為
,切線方程為![]() .
.
令![]() ,得
,得![]() ,即點
,即點![]() 在線段
在線段![]() 上且距離
上且距離![]() 軸
軸![]() 百米.
百米.
答:當點![]() 在線段
在線段![]() 上且距離
上且距離![]() 軸
軸![]() 百米,通道PQ最短.
百米,通道PQ最短.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]
在直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為![]()
![]() 為參數
為參數![]() 以原點為極點x軸正半軸為極軸建立極坐標系,直線
以原點為極點x軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為:
的極坐標方程為:![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 的極坐標方程,并指出它是何種曲線;
的極坐標方程,并指出它是何種曲線;
(Ⅱ)設![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,
兩點,![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著小汽車的普及,“駕駛證”已經成為現代人“必考”證件之一.若某人報名參加了駕駛證考試,要順利地拿到駕駛證,需要通過四個科目的考試,其中科目二為場地考試在每一次報名中,每個學員有![]() 次參加科目二考試的機會(這
次參加科目二考試的機會(這![]() 次考試機會中任何一次通過考試,就算順利通過,即進入下一科目考試,或
次考試機會中任何一次通過考試,就算順利通過,即進入下一科目考試,或![]() 次都沒有通過,則需要重新報名),其中前
次都沒有通過,則需要重新報名),其中前![]() 次參加科目二考試免費,若前
次參加科目二考試免費,若前![]() 次都沒有通過,則以后每次參加科目二考試都需要交
次都沒有通過,則以后每次參加科目二考試都需要交![]() 元的補考費.某駕校通過幾年的資料統計,得到如下結論:男性學員參加科目二考試,每次通過的概率均為
元的補考費.某駕校通過幾年的資料統計,得到如下結論:男性學員參加科目二考試,每次通過的概率均為![]() ,女性學員參加科目二考試,每次通過的概率均為
,女性學員參加科目二考試,每次通過的概率均為![]() .現有一對夫妻同時報名參加駕駛證考試,在本次報名中,若這對夫妻參加科目二考試的原則為:通過科目二考試或者用完所有機會為止.
.現有一對夫妻同時報名參加駕駛證考試,在本次報名中,若這對夫妻參加科目二考試的原則為:通過科目二考試或者用完所有機會為止.
(1)求這對夫妻在本次報名中參加科目二考試都不需要交補考費的概率;
(2)求這對夫妻在本次報名中參加科目二考試產生的補考費用之和為![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(題文)已知拋物線![]() 和圓
和圓![]() 的公共弦過拋物線的焦點
的公共弦過拋物線的焦點![]() ,且弦長為4.
,且弦長為4.
(1)求拋物線和圓的方程;
(2)過點![]() 的直線與拋物線相交于
的直線與拋物線相交于![]() 兩點拋物線在點
兩點拋物線在點![]() 處的切線與
處的切線與![]() 軸的交點為
軸的交點為![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
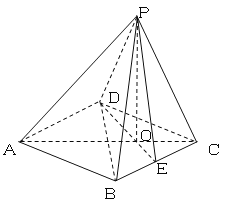
【題目】如圖,已知四棱錐P-ABCD的底面是邊長為2的菱形,∠BCD=60°,點E是BC邊
的中點,AC,DE交于點O,![]() ,且PO⊥平面ABCD.
,且PO⊥平面ABCD.
(1)求證:PD⊥BC;
(2)在線段AP上找一點F,使得BF∥平面PDE,并求此時四面體PDEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 的離心率為
的離心率為![]() ,并且橢圓經過點P(1,
,并且橢圓經過點P(1,![]() ),直線l的方程為x=4.
),直線l的方程為x=4.
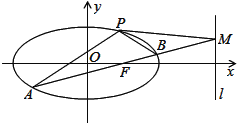
(1)求橢圓的方程;
(2)已知橢圓內一點E(1,0),過點E作一條斜率為k的直線與橢圓交于A,B兩點,交直線l于點M,記PA,PB,PM的斜率分別為k1,k2,k3.問:是否存在常數![]() ,使得k1+k2=
,使得k1+k2=![]() k3?若存在,求出
k3?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 數列
數列![]() 的前
的前![]() 項和,對任意
項和,對任意![]() ,都有
,都有![]() (
(![]() 為常數).
為常數).
(1)當![]() 時,求
時,求![]() ;
;
(2)當![]() 時,
時,
(ⅰ)求證:數列![]() 是等差數列;
是等差數列;
(ⅱ)若對任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中點點P在線段A1B上.
2,AB⊥AC,M是棱BC的中點點P在線段A1B上.
(1)若P是線段A1B的中點,求直線MP與直線AC所成角的大小;
(2)若![]() 是
是![]() 的中點,直線
的中點,直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段BP的長度.
,求線段BP的長度.

查看答案和解析>>
科目:高中數學 來源: 題型:
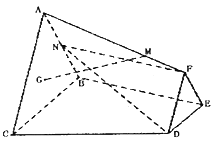
【題目】如圖,已知![]() 與
與![]() 分別是邊長為1與2的正三角形,
分別是邊長為1與2的正三角形,![]() ,四邊形
,四邊形![]() 為直角梯形,且
為直角梯形,且![]() ,
,![]() ,點
,點![]() 為
為![]() 的重心,
的重心,![]() 為
為![]() 中點,
中點,![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 上靠近點
上靠近點![]() 的三等分點.
的三等分點.
(1)求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,試求異面直線
,試求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com