
為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
| 性別 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
 的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關? | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |

(1)老年人的比例的估算值為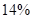 ;(2)有
;(2)有 的把握認為該地區的老年人是否需要幫助與性別有關;(3)采用分層抽樣的方法比采用簡單隨機抽樣方法好.
的把握認為該地區的老年人是否需要幫助與性別有關;(3)采用分層抽樣的方法比采用簡單隨機抽樣方法好.
解析試題分析:(1)根據調查結果,用需要幫助的人數除以調查的總人數去估計需要幫助的老年人的比例即可;(2)根據提供的數據,根據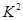 的計算公式先得到
的計算公式先得到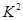 的觀測值,進而跟
的觀測值,進而跟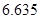 比較,如果比
比較,如果比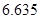 大,就可能認為有
大,就可能認為有 的把握認為該地區的老年人是否需要幫助與性別有關,否則沒有;(3)因為該地區男性老年人與女性老年人中需要幫助的比例有明顯差異,所以采用分層抽樣更好.
的把握認為該地區的老年人是否需要幫助與性別有關,否則沒有;(3)因為該地區男性老年人與女性老年人中需要幫助的比例有明顯差異,所以采用分層抽樣更好.
(1)調查的500位老年人中有70位需要志愿者提供幫助,因此該地區老年人中,需要幫助的老年人的比例的估算值為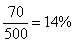 5分
5分
(2)根據表中數據可計算得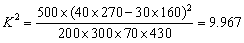
由于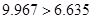 ,所以有
,所以有 的把握認為該地區的老年人是否需要幫助與性別有關 10分
的把握認為該地區的老年人是否需要幫助與性別有關 10分
(3)由(2)的結論知,該地區老年人是否需要幫助與性別有關,并且從樣本數據能看出該地區男性老年人與女性老年人中需要幫助的比例有明顯差異,因此在調查時,先確定該地區老年人中男、女的比例,再把老年人分成男、女兩層并采用分層抽樣方法比采用簡單隨機抽樣方法更好 12分.
考點:1.古典概型;2.獨立性檢驗;3.隨機抽樣.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
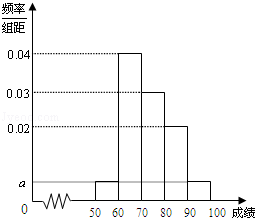
某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求圖中 的值;
的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.
| 分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,從參加環保知識競賽的學生中抽出60名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:請觀察圖形,求解下列問題:
(1)79.5~89.5這一組的頻率、頻數分別是多少?
(2)估計這次環保知識競賽的及格率(60分及以上為及格)和平均分.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某高校在2012年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組得到的頻率分布表如下圖所示,
| 班號 | 分組 | 頻數 | 頻率 |
| 第1組 | 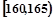 | 5 | 0.050 |
| 第2組 | 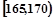 | ① | 0.350 |
| 第3組 | 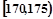 | 30 | ② |
| 第4組 | 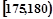 | 20 | 0.200 |
| 第5組 | 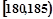 | 10 | 0.100 |
| 合計 | 100 | 1.00 | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某校隨機抽取100名學生,獲得了他們一周課外閱讀時間(單位:小時)的數據,整理得到數據分組及頻數分布表和頻率分布直方圖:
(1)從該校隨機選取一名學生,試估計這名學生該周課外閱讀時間少于12小時的概率;
(2)求頻率分布直方圖中的a,b的值;
(3)假設同一組中的每個數據可用該組區間的中點值代替,試估計樣本中的100名學生該周課外閱讀時間的平均數在第幾組(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學的數學測試中設置了“數學與邏輯”和“閱讀與表達”兩個內容,成績分為A、B、C、D、E五個等級。某班考生兩科的考試成績的數據統計如圖所示,其中“數學與邏輯”科目的成績等級為B的考生有10人
(1)求該班考生中“閱讀與表達”科目中成績等級為A的人數;
(2)若等級A、B、C、D、E分別對應5分、4分、3分、2分、1分,該考場中有2人10分,3人9分,從這5人中隨機抽取2人,求2人成績之和為19分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某數學興趣小組有男女生各 名.以下莖葉圖記錄了該小組同學在一次數學測試中的成績(單位:分).已知男生數據的中位數為
名.以下莖葉圖記錄了該小組同學在一次數學測試中的成績(單位:分).已知男生數據的中位數為 ,女生數據的平均數為
,女生數據的平均數為 .
.
(1)求 ,
, 的值;
的值;
(2)現從成績高于 分的同學中隨機抽取兩名同學,求抽取的兩名同學恰好為一男一女的概率.
分的同學中隨機抽取兩名同學,求抽取的兩名同學恰好為一男一女的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分 )
2013年國慶期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下圖的頻率分布直方圖.
后得到如下圖的頻率分布直方圖.
(1)此調查公司在采樣中,用到的是什么抽樣方法?
(2)求這40輛小型車輛車速的中位數的估計值;
(3)若從車速在 的車輛中任抽取3輛,求抽出的3輛車中車速在
的車輛中任抽取3輛,求抽出的3輛車中車速在 的車輛數
的車輛數 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為迎接6月6日的“全國愛眼日”,某高中學生會從全體學生中隨機抽取16名學生,經校醫用對數視力表檢查得到每個學生的視力狀況的莖葉圖(以小數點前的一位數字為莖,小數點后的一位數字為葉),如圖,若視力測試結果不低于5.0,則稱為“好視力”.
(1)寫出這組數據的眾數和中位數;
(2)從這16人中隨機選取3人,求至少有2人是“好視力”的概率;
(3)以這16人的樣本數據來估計整個學校的總體數據,若從該校(人數很多)任選3人,記X表示抽到“好視力”學生的人數,求X的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com