【題目】如圖，已知正四棱錐P﹣ABCD中，PA=AB=2，點M，N分別在PA，BD上，且 
= 
． 
（1）求異面直線MN與PC所成角的大小；
（2）求二面角N﹣PC﹣B的余弦值．
【答案】
（1）解：設AC與BD的交點為O，AB=PA=2．以點O為坐標原點，
， 
， 
方向分別是x軸、y軸、z軸正方向，建立空間直角坐標系O﹣xyz．
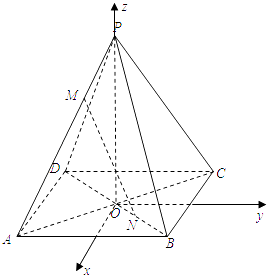
則A（1，﹣1，0），B（1，1，0），C（﹣1，1，0），D（﹣1，﹣1，0），…（2分）
設P（0，0，p），則 
=（﹣1，1，p），又AP=2，
∴1+1+p2=4，∴p= 
，
∵ 
= 
= 
=（ 
），
=（ 
），
∴ 
=（﹣1，1，﹣ ）， 
=（0， 
，﹣ 
），
設異面直線MN與PC所成角為θ，
則cosθ=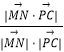 
= 
= 
．
θ=30°，
∴異面直線MN與PC所成角為30°
（2）解： =（﹣1，1，﹣ ）， 
=（1，1，﹣ ）， 
=（ 
, ，﹣ ），
設平面PBC的法向量 
=（x，y，z），
則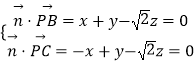 
，取z=1，得 =（0， ，1），
設平面PNC的法向量 
=（a，b，c），
則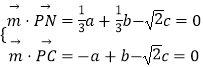 
，取c=1，得 =（ ，2 ，1），
設二面角N﹣PC﹣B的平面角為θ，
則cosθ= 
= 
= 
．
∴二面角N﹣PC﹣B的余弦值為 ．
【解析】（1）設AC與BD的交點為O，AB=PA=2．以點O為坐標原點， ， ， 方向分別是x軸、y軸、z軸正方向，建立空間直角坐標系O﹣xyz．利用向量法能求出異面直線MN與PC所成角．（2）求出平面PBC的法向量和平面PNC的法向量，利用向量法能求出二面角N﹣PC﹣B的余弦值．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax3+cx（a＞0），其圖象在點（1，f（1））處的切線與直線 x﹣6y+21=0垂直，導函數
f′（x）的最小值為﹣12．
（1）求函數f（x）的解析式；
（2）求y=f（x）在x∈[﹣2，2]的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知橢圓 
=l （a＞b＞0）的焦距為2，離心率為 
，橢圓的右頂點為A．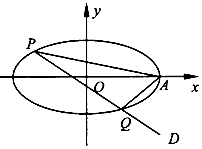
（1）求該橢圓的方程：
（2）過點D（ 
，﹣ ）作直線PQ交橢圓于兩個不同點P，Q，求證：直線AP，AQ的
斜率之和為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二階矩陣M有特征值λ=8及對應的一個特征向量 
=[ 
]，并且矩陣M對應的變換將點（﹣1，2）變換成（﹣2，4）．
（1）求矩陣M；
（2）求矩陣M的另一個特征值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓O1和圓O2的極坐標方程分別為ρ=2， 
．
（1）把圓O1和圓O2的極坐標方程化為直角坐標方程；
（2）求經過兩圓交點的直線的極坐標方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】閱讀如下程序框圖，如果輸出i=5，那么在空白矩形框中應填入的語句為（ ）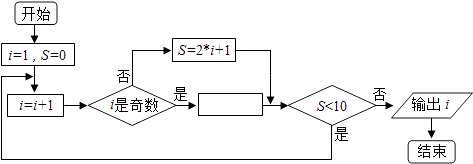 
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
為正方形， 
底面
， 
，過點
的平面與棱
， 
， 
分別交于點
， 
， 
（
， 
， 
三點均不在棱的端點處）．
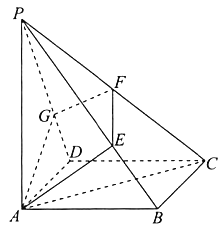
（Ⅰ）求證：平面
平面
；
（Ⅱ）若
平面
，求
的值；
（Ⅲ）直線
是否可能與平面
平行？證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙、丙三人進行羽毛球練習賽，其中兩人比賽，另一人當裁判，每局比賽結束時，負的一方在下一局當裁判，設各局中雙方獲勝的概率均為 
，各局比賽的結果都相互獨立，第1局甲當裁判．
（1）求第4局甲當裁判的概率；
（2）X表示前4局中乙當裁判的次數，求X的數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
