
【題目】已知函數![]() .
.
(1)求函數![]() 在區間
在區間![]() 上的最小值
上的最小值![]() ;
;
(2)令![]()
![]() 是函數
是函數![]() 圖象上任意兩點,且滿足
圖象上任意兩點,且滿足![]() 求實數
求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,使
,使![]() 成立,求實數
成立,求實數![]() 的最大值.
的最大值.
【答案】(1)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .(2)
.(2)![]() (3)
(3)![]() .
.
【解析】
試題分析:(1)先求導數![]() ,再求導函數零點
,再求導函數零點![]() ,根據零點與定義區間位置關系分類討論函數單調性:當
,根據零點與定義區間位置關系分類討論函數單調性:當![]() 時,
時,![]() 在
在![]() 上單調遞增,當
上單調遞增,當![]() 時,
時,![]() 在區間
在區間![]() 上為減函數,在區間
上為減函數,在區間![]() 上為增函數,最后根據單調性確定函數最小值(2)先轉化不等式
上為增函數,最后根據單調性確定函數最小值(2)先轉化不等式![]() 不妨取
不妨取![]() ,則
,則![]() ,即
,即![]() 恒成立,即
恒成立,即![]() 在
在![]() 上單調遞增,然后利用導數研究函數單調性:
上單調遞增,然后利用導數研究函數單調性:![]() 在
在![]() 恒成立.最后利用變量分離轉化為對應函數最值,求參數.(3)不等式有解問題與恒成立問題一樣,先利用變量分離轉化為對應函數最值,
恒成立.最后利用變量分離轉化為對應函數最值,求參數.(3)不等式有解問題與恒成立問題一樣,先利用變量分離轉化為對應函數最值,![]() 的最大值,再利用導數求函數
的最大值,再利用導數求函數![]() 的最值,這要用到二次求導,才可確定函數單調性:
的最值,這要用到二次求導,才可確定函數單調性:![]() 在
在![]() 上單調遞增,進而確定函數最值
上單調遞增,進而確定函數最值
試題解析:解(1)![]() ,令
,令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() 的最小值為
的最小值為![]() ;
;
當![]() 時,
時,![]() 在區間
在區間![]() 上為減函數,在區間
上為減函數,在區間![]() 上為增函數,
上為增函數,
![]() 的最小值為
的最小值為![]() .
.
綜上,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
(2)![]() ,對于任意的
,對于任意的![]() ,不妨取
,不妨取![]() ,則
,則![]() ,
,
則由![]() 可得
可得![]() ,
,
變形得![]() 恒成立,
恒成立,
令![]() ,
,
則![]() 在
在![]() 上單調遞增,
上單調遞增,
故![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 恒成立.
恒成立.
![]() ,當且僅當
,當且僅當![]() 時取
時取![]() ,
,
![]() .
.
(3)![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() 使得
使得![]() 成立.
成立.
令![]() ,則
,則![]() ,
,
令![]() ,則由
,則由![]() 可得
可得![]() 或
或![]() (舍)
(舍)
當![]() 時
時![]() ,則
,則![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時
時![]() ,則
,則![]() 在
在![]() 上單調遞增.
上單調遞增.
![]()
![]() 在
在![]() 上恒成立.
上恒成立.
![]() 在
在![]() 上單調遞增.
上單調遞增.
![]() ,即
,即![]() .
.
![]() 實數
實數![]() 的最大值為
的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某社會機構為了調查對手機游戲的興趣與年齡的關系,通過問卷調查,整理數據得如下![]() 列聯表:
列聯表:

(1)根據列聯表,能否有99.9%的把握認為對手機游戲的興趣程度與年齡有關?
(2)若已經從40歲以下的被調查者中用分層抽樣的方式抽取了5名,現從這5名被調查者中隨機選取3名,求這3名被調查者中恰有1名對手機游戲無興趣的概率.
附: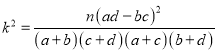
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() ≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某沿海地區計劃鋪設一條電纜聯通A,B兩地,A地位于東西方向的直線MN上的陸地處,B地位于海上一個燈塔處,在A地用測角器測得![]() ,在A地正西方向4km的點C處,用測角器測得
,在A地正西方向4km的點C處,用測角器測得![]() .擬定鋪設方案如下:在岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設.預算地下、水下的電纜鋪設費用分別為2萬元/km和4萬元/km,設
.擬定鋪設方案如下:在岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設.預算地下、水下的電纜鋪設費用分別為2萬元/km和4萬元/km,設![]() ,
,![]() ,鋪設電纜的總費用為
,鋪設電纜的總費用為![]() 萬元.
萬元.
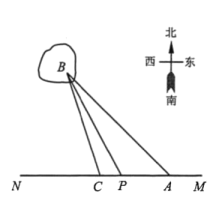
(1)求函數![]() 的解析式;
的解析式;
(2)試問點P選在何處時,鋪設的總費用最少,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中無理數
,其中無理數![]() .
.
(Ⅰ)若函數![]() 有兩個極值點,求
有兩個極值點,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數![]() 的極值點有三個,最小的記為
的極值點有三個,最小的記為![]() ,最大的記為
,最大的記為![]() ,若
,若![]() 的最大值為
的最大值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() ,點
,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax2-a-lnx,其中a ∈R.
(I)討論f(x)的單調性;
(II)確定a的所有可能取值,使得![]() 在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數)。
在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數)。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是各項均為正數的等比數列,
是各項均為正數的等比數列,![]() 是等差數列,且
是等差數列,且![]() .
.
(I)求![]() 和
和![]() 的通項公式;
的通項公式;
(II)設數列![]() 滿足
滿足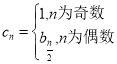 ,求
,求![]() ;
;
(III)對任意正整數![]() ,不等式
,不等式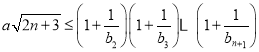 成立,求正數
成立,求正數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com