
【題目】已知函數f(x)=(a﹣ ![]() )x2+lnx(a為實數).
)x2+lnx(a為實數).
(1)當a=0時,求函數f(x)在區間[ ![]() ,e]上的最大值和最小值;
,e]上的最大值和最小值;
(2)若對任意的x∈(1,+∞),g(x)=f(x)﹣2ax<0恒成立,求實數a的取值范圍.
【答案】
(1)解:當a=0時,函數f(x)=﹣ ![]() ,(x>0)
,(x>0)
f′(x)=﹣x+ ![]() =
= ![]() ,(x>0),令f′(x)=0,得x=1,(負值舍去)
,(x>0),令f′(x)=0,得x=1,(負值舍去)
∴x>0,x、f′(x),f(x)的變化如下:
x | ( | 1 | (1,e) |
f′(x) | + | 0 | |
f(x) | ↑ | 極大值 | ↓ |
∴f(x)在( ![]() ,1)上單調遞增,在(1,e)上單調遞減,
,1)上單調遞增,在(1,e)上單調遞減,
f(x)最大值為f(1)= ![]() .
.
∵ ![]() ,∴f(x)最小值為f(e)=1﹣
,∴f(x)最小值為f(e)=1﹣ ![]()
(2)解:g(x)=f(x)﹣2ax=(a﹣ ![]() )x2+lnx﹣2ax,g(x)的定義域為(0,+∞),
)x2+lnx﹣2ax,g(x)的定義域為(0,+∞),
![]()
①若a ![]() ,令g′(x)=0,得極值x1=1,x2=
,令g′(x)=0,得極值x1=1,x2= ![]() ,
,
當x1<x2,即 ![]() 時,在(0,1)上有g′(x)>0,
時,在(0,1)上有g′(x)>0,
在(1,x2)上有g′(x)<0,
在(x2,+∞)上有g′(x)>0,此時g(x)在區間(x2,+∞)上是增函數,
并且在該區間上有g(x)∈(g(x2),+∞)不合題意;
當x2≤x1,即a≥1時,同理可知,g(x)在區間(1,+∞)上,
有g(x)∈(g(1),+∞),也不合題意;
②若a≤ ![]() ,則有x1>x2,此時在區間(1,+∞)上恒有g′(x)<0,
,則有x1>x2,此時在區間(1,+∞)上恒有g′(x)<0,
從而g(x)在區間(1,+∞)上是減函數;
要使g(x)<0在此區間上恒成立,只須滿足g(1)=﹣a﹣ ![]() ≤0,得a≥﹣
≤0,得a≥﹣ ![]()
由此求得a的范圍是[﹣ ![]() ,
, ![]() ]
]
綜合①②可知實數a的取值范圍是[﹣ ![]() ,
, ![]() ]
]
【解析】(1)求出導數,由此能求出f(x)在(0,1)上單調遞增,在(1,+∞))上單調遞減.f(x)在( ![]() ,1)上單調遞增,在(1,e)上單調遞減,由此能求出f(x)在區間[
,1)上單調遞增,在(1,e)上單調遞減,由此能求出f(x)在區間[ ![]() ,e]上的最大值和最小值.(2)求出函數g(x)的導數,討論①若a
,e]上的最大值和最小值.(2)求出函數g(x)的導數,討論①若a ![]() ,②若a≤
,②若a≤ ![]() ,求得單調區間,可得g(x)的范圍,由恒成立思想,進而得到a的范圍.
,求得單調區間,可得g(x)的范圍,由恒成立思想,進而得到a的范圍.
【考點精析】根據題目的已知條件,利用利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識可以得到問題的答案,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】下列函數中,滿足“f(x+y)=f(x)f(y)”的單調遞增函數是( )
A.f(x)=x3
B.f(x)=x ![]()
C.f(x)=3x
D.f(x)=( ![]() )x
)x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos(2x ![]() )﹣2sin(x
)﹣2sin(x ![]() )cos(x
)cos(x ![]() )
)
(1)求函數f(x)的最小正周期; (Ⅱ)求函數f(x)在區間[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,一個圓錐形的空杯子上放著一個直徑為8cm的半球形的冰淇淋,請你設計一種這樣的圓錐形杯子(杯口直徑等于半球形的冰淇淋的直徑,杯子壁厚忽略不計),使冰淇淋融化后不會溢出杯子,怎樣設計最省材料?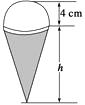
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 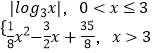 ,若函數g(x)=f(x)﹣m存在4個不同的零點x1 , x2 , x3 , x4 , 則實數m的取值范圍是 , x1x2x3x4的取值范圍是 .
,若函數g(x)=f(x)﹣m存在4個不同的零點x1 , x2 , x3 , x4 , 則實數m的取值范圍是 , x1x2x3x4的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設 ![]() 是兩條不同的直線,
是兩條不同的直線, ![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若 ![]() ,則
,則 ![]() ②若
②若 ![]() ,則
,則 ![]()
③若 ![]() ,則
,則 ![]() ④若
④若 ![]() ,則
,則 ![]()
其中正確命題的序號是( )
A.①和②
B.②和③
C.③和④
D.①和④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=4x焦點為F,點D為其準線與x軸的交點,過點F的直線l與拋物線相交于A,B兩點,則△DAB的面積S的取值范圍為( )
A.[5,+∞)
B.[2,+∞)
C.[4,+∞)
D.[2,4]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知N為自然數集,集合P={1,4,7,10,13},Q={2,4,6,8,10},則P∩ ![]() 等于( )
等于( )
A.{1,7,13}
B.{4,10}
C.{1,7}
D.{0,1,3}
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com