
【題目】已知函數![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)若![]() ,
,![]() 是
是![]() 的兩個零點,求證:
的兩個零點,求證:![]() .
.
【答案】(1)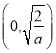 上單調遞減,
上單調遞減,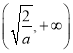 上單調遞增.(2)證明見解析
上單調遞增.(2)證明見解析
【解析】
(1)對函數![]() 求導,求出
求導,求出![]() 的解,即可得出結論;
的解,即可得出結論;
(2)由(1)求出函數有兩解滿足的條件,再利用零點存在性定理求出其中一個零點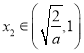 ,要證
,要證![]() ,只需證
,只需證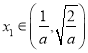 ,即證
,即證![]() ,根據
,根據![]() 式子特征,通過構造函數
式子特征,通過構造函數![]() ,
,![]() ,證明
,證明![]() ,得出
,得出![]() ,即可證明結論.
,即可證明結論.
(1)由條件可知,函數![]() 的定義域是
的定義域是![]() .
.
由![]() 可得
可得![]() .
.
當![]() 時,當
時,當![]() 時,
時,![]() ;當
;當![]() 時,
時,
![]() ,則
,則![]() 在
在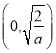 上單調遞減,
上單調遞減,
在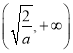 上單調遞增.
上單調遞增.
(2)當![]() 時,
時,![]() 在
在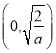 上單調遞減,
上單調遞減,
在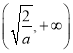 上單調遞增.所
上單調遞增.所![]() ,
,
①當![]() 時,即
時,即![]() ,
,
此時![]() 至多1個零點,故不滿足條件;
至多1個零點,故不滿足條件;
②當![]() ,即
,即![]() ,即
,即![]() ,
,
因為![]() 在
在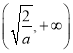 上單調遞增且
上單調遞增且![]() ,
,
所以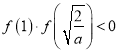 ,
,
所以![]() 在
在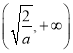 上有且只有1個零點
上有且只有1個零點![]() ,
,
則![]() ;
;
當![]() 時,令
時,令![]() ,
,
則![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
在![]() 上單調遞增.所以
上單調遞增.所以![]() ,
,
所以![]() ,
,![]() ,
,
又因為當![]() 時,所以
時,所以![]() ,
,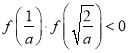 ,
,
又因為![]() 在
在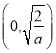 上單調遞減,
上單調遞減,
所以![]() 在
在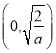 有且只有一個零點,
有且只有一個零點,
則![]() ,所以
,所以![]() ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數據,繪制了如圖所示的折線圖.根據該折線圖,下列結論錯誤的是( )
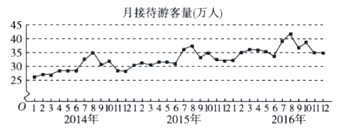
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an}的前n項和為Sn,且an2+2an=4Sn﹣1(n∈N*).
(1)求數列{an}的通項公式;
(2)若bn![]() ,數列{bn}的前n項和為Tn,求Tn的取值范圍.
,數列{bn}的前n項和為Tn,求Tn的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高二年級學生中隨機抽取60名學生,將其期中考試的政治成績(均為整數)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下頻率分布直方圖.
后得到如下頻率分布直方圖.

(1)根據頻率分布直方圖,估計該校高二年級學生期中考試政治成績的平均分、眾數、中位數;(小數點后保留一位有效數字)
(2)用分層抽樣的方法在各分數段的學生中抽取一個容量為20的樣本,則各分數段抽取的人數分別是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校共有6個學生餐廳,甲、乙、丙、丁四位同學每人隨機地選擇一家餐廳就餐(選擇到每個餐廳概率相同),則下列結論正確的是( )
A.四人去了四個不同餐廳就餐的概率為![]()
B.四人去了同一餐廳就餐的概率為![]()
C.四人中恰有2人去了第一餐廳就餐的概率為![]()
D.四人中去第一餐廳就餐的人數的期望為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 分別為橢圓
分別為橢圓![]() 的焦點,直線
的焦點,直線![]() :
:![]() 與
與![]() 軸交于
軸交于![]() 點,若
點,若![]() ,且
,且![]() .
.

(1)求橢圓的方程;
(2)過![]() ,
,![]() 作互相垂直的兩直線分別與橢圓交于
作互相垂直的兩直線分別與橢圓交于![]() ,
,![]() ,
,![]() ,
,![]() 四點,求四邊形
四點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:![]() )得頻率分布直方圖如下:
)得頻率分布直方圖如下:


(1)設兩種養殖方法的箱產量相互獨立,記![]() 表示事件:“舊養殖法的箱產量低于
表示事件:“舊養殖法的箱產量低于![]() ,新養殖法的箱產量不低于
,新養殖法的箱產量不低于![]() ”,估計
”,估計![]() 的概率;
的概率;
(2)填寫下面![]() 列聯表,并根據聯表判斷是否有
列聯表,并根據聯表判斷是否有![]() 的把握認為箱產量與養殖方法有關:
的把握認為箱產量與養殖方法有關:
箱產量 | 箱產量 | |
舊養殖法 | ||
新養殖法 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)根據箱產量的頻率分布直方圖,求新養殖法箱產量的中位數的估計值(精確到0.01)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列結論:在回歸分析中
(1)可用相關指數![]() 的值判斷模型的擬合效果,
的值判斷模型的擬合效果,![]() 越大,模型的擬合效果越好;
越大,模型的擬合效果越好;
(2)可用殘差平方和判斷模型的擬合效果,殘差平方和越大,模型的擬合效果越好;
(3)可用相關系數![]() 的值判斷模型的擬合效果,
的值判斷模型的擬合效果,![]() 越大,模型的擬合效果越好;
越大,模型的擬合效果越好;
(4)可用殘差圖判斷模型的擬合效果,殘差點比較均勻地落在水平的帶狀區域中,說明這樣的模型比較合適.帶狀區域的寬度越窄,說明模型的擬合精度越高.
以上結論中,不正確的是( )
A.(1)(3)B.(2)(3)C.(1)(4)D.(3)(4)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com