
【題目】設(shè)圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() 且與
且與![]() 軸不重合,交圓
軸不重合,交圓![]() 于
于![]() ,
,![]() 兩點(diǎn),過(guò)點(diǎn)
兩點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 的平行線交
的平行線交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求![]() 的值;
的值;
(2)設(shè)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),與直線
兩點(diǎn),與直線![]() 相交于
相交于![]() 點(diǎn),試問(wèn)在橢圓
點(diǎn),試問(wèn)在橢圓![]() 上是否存在一定點(diǎn)
上是否存在一定點(diǎn)![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差數(shù)列(其中
成等差數(shù)列(其中![]() ,
,![]() ,
,![]() 分別指直線
分別指直線![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 點(diǎn)的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
點(diǎn)的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
【答案】(1) ![]() (2)見證明
(2)見證明
【解析】
(1)由![]() 且
且![]() ,可得
,可得![]() ,進(jìn)而得到
,進(jìn)而得到![]()
![]() ,再由半徑
,再由半徑![]() ,即可求解;
,即可求解;
(2)由(1)知得![]() 的方程,設(shè)直線
的方程,設(shè)直線![]() 的方程為
的方程為![]() ,代入橢圓的方程,利用根與系數(shù)的關(guān)系和
,代入橢圓的方程,利用根與系數(shù)的關(guān)系和![]() ,
,![]() ,
,![]() 成等差數(shù)列,求得
成等差數(shù)列,求得![]()
![]() ,由對(duì)任意的
,由對(duì)任意的![]() 該等式恒成立,求得
該等式恒成立,求得![]() ,即可得到答案.
,即可得到答案.
(1)因?yàn)閳A![]() 的圓心為
的圓心為![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因?yàn)閳A![]() 的半徑為8,即
的半徑為8,即![]() ,
,
所以![]() .
.
(2)由(1)知,曲線![]() 是以
是以![]() ,
,![]() 為焦點(diǎn)的橢圓,且長(zhǎng)軸長(zhǎng)為8,
為焦點(diǎn)的橢圓,且長(zhǎng)軸長(zhǎng)為8,
所以曲線![]() 的方程為
的方程為![]() ,
,
設(shè)直線![]() 的方程為
的方程為![]() ,
,
代入橢圓化簡(jiǎn)得![]() ,
,
設(shè)![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
所以![]()
![]()
 ,
,
因?yàn)?/span>![]() ,
,![]() ,
,![]() 成等差數(shù)列,所以
成等差數(shù)列,所以![]() ,
,
因?yàn)?/span>![]() ,所以
,所以![]()
 ,
,
化簡(jiǎn)得![]() ,
,
對(duì)任意的![]() 該等式恒成立,所以
該等式恒成立,所以![]() ,
,
所以存在點(diǎn)![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差數(shù)列.
成等差數(shù)列.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求證:函數(shù)![]() 是偶函數(shù);
是偶函數(shù);
(2)設(shè)![]() ,求關(guān)于
,求關(guān)于![]() 的函數(shù)
的函數(shù)![]() 在
在![]() 時(shí)的值域
時(shí)的值域![]() 的表達(dá)式;
的表達(dá)式;
(3)若關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 時(shí)恒成立,求實(shí)數(shù)
時(shí)恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某歌手大賽進(jìn)行電視直播,比賽現(xiàn)場(chǎng)有6名特約嘉賓給每位參賽選手評(píng)分,場(chǎng)內(nèi)外的觀眾可以通過(guò)網(wǎng)絡(luò)平臺(tái)給每位參賽選手評(píng)分.某選手參加比賽后,現(xiàn)場(chǎng)嘉賓評(píng)分情況如下表;場(chǎng)內(nèi)外共有數(shù)萬(wàn)名觀眾參與了評(píng)分,組織方將觀眾評(píng)分按照![]() ,
,![]() ,
,![]() 分組,繪成頻率分布直方圖如下:
分組,繪成頻率分布直方圖如下:
嘉賓 |
|
|
|
|
|
|
評(píng)分 | 96 | 95 | 96 | 89 | 97 | 98 |
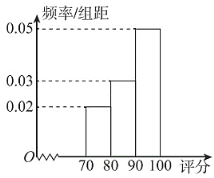
(1)從觀眾中任取三人,求這三人中恰有1人分?jǐn)?shù)在![]() 另2人分?jǐn)?shù)在
另2人分?jǐn)?shù)在![]() 的概率;
的概率;
(2)從嘉賓中隨機(jī)選3人,記3人中分?jǐn)?shù)不低于96分的人數(shù)為![]() ,求
,求![]() 的期望;
的期望;
(3)嘉賓評(píng)分的平均數(shù)為![]() ,場(chǎng)內(nèi)外的觀眾評(píng)分的平均數(shù)為
,場(chǎng)內(nèi)外的觀眾評(píng)分的平均數(shù)為![]() 與
與![]() 的大小關(guān)系(不需要證明).
的大小關(guān)系(不需要證明).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 、
、![]() 是橢圓
是橢圓![]() 的左、右頂點(diǎn),
的左、右頂點(diǎn),![]() 為橢圓上異于
為橢圓上異于![]() 、
、![]() 的一點(diǎn).
的一點(diǎn).
(1)![]() 是橢圓
是橢圓![]() 的上頂點(diǎn),且直線
的上頂點(diǎn),且直線![]() 與直線
與直線![]() 垂直,求點(diǎn)
垂直,求點(diǎn)![]() 到
到![]() 軸的距離;
軸的距離;
(2)過(guò)點(diǎn)![]() 的直線
的直線![]() (不過(guò)坐標(biāo)原點(diǎn))與橢圓
(不過(guò)坐標(biāo)原點(diǎn))與橢圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),且點(diǎn)
兩點(diǎn),且點(diǎn)![]() 在
在![]() 軸上方,點(diǎn)
軸上方,點(diǎn)![]() 在
在![]() 軸下方,若
軸下方,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .其中
.其中![]() 是自然對(duì)數(shù)的底數(shù).
是自然對(duì)數(shù)的底數(shù).
(1)求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)若不等式![]() 對(duì)任意的
對(duì)任意的![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)橢圓E:![]() (a,b>0)過(guò)M(2,
(a,b>0)過(guò)M(2,![]() ) ,N(
) ,N(![]() ,1)兩點(diǎn),O為坐標(biāo)原點(diǎn),
,1)兩點(diǎn),O為坐標(biāo)原點(diǎn),
(1)求橢圓E的方程;
(2)是否存在圓心在原點(diǎn)的圓,使得該圓的任意一條切線與橢圓E恒有兩個(gè)交點(diǎn)A,B,且![]() ?若存在,寫出該圓的方程,若不存在說(shuō)明理由.
?若存在,寫出該圓的方程,若不存在說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】維生素C又叫抗壞血酸,是一種水溶性維生素,是高等靈長(zhǎng)類動(dòng)物與其他少數(shù)生物的必需營(yíng)養(yǎng)素.維生素C雖不直接構(gòu)成腦組織,也不向腦提供活動(dòng)能源,但維生素C有多種健腦強(qiáng)身的功效,它是腦功能極為重要的營(yíng)養(yǎng)物.維生素C的毒性很小,但食用過(guò)多仍可產(chǎn)生一些不良反應(yīng).根據(jù)食物中維C的含量可大致分為:含量很豐富:鮮棗、沙棘、獼猴桃、柚子,每100克中的維生素C含量超過(guò)100毫克;比較豐富:青椒、桂圓、番茄、草莓、甘藍(lán)、黃瓜、柑橘、菜花,每100克中維生素C含量超過(guò)50毫克;相對(duì)豐富:白菜、油菜、香菜、菠菜、芹菜、莧菜、菜苔、豌豆、豇豆、蘿卜,每100克中維生素C含量超過(guò)30~50毫克.現(xiàn)從獼猴桃、柚子兩種食物中測(cè)得每100克所含維生素C的量(單位:![]() )得到莖葉圖如圖所示,則下列說(shuō)法中不正確的是( )
)得到莖葉圖如圖所示,則下列說(shuō)法中不正確的是( )
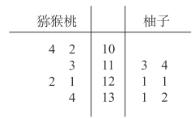
A.獼猴桃的平均數(shù)小于柚子的平均數(shù)
B.獼猴桃的方差小于柚子的方差
C.獼猴桃的極差為32
D.柚子的中位數(shù)為121
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的短軸長(zhǎng)為
的短軸長(zhǎng)為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若動(dòng)直線![]() 與橢圓
與橢圓![]() 有且僅有一個(gè)公共點(diǎn),分別過(guò)
有且僅有一個(gè)公共點(diǎn),分別過(guò)![]() 兩點(diǎn)作
兩點(diǎn)作![]() ,垂足分別為
,垂足分別為![]() ,且記
,且記![]() 為點(diǎn)
為點(diǎn)![]() 到直線
到直線![]() 的距離,
的距離, ![]() 為點(diǎn)
為點(diǎn)![]() 到直線
到直線![]() 的距離,
的距離,![]() 為點(diǎn)
為點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離,試探索
的距離,試探索![]() 是否存在最大值.若存在,求出最大值;若不存在,請(qǐng)說(shuō)明理由.
是否存在最大值.若存在,求出最大值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,
,![]() 軸上方的點(diǎn)
軸上方的點(diǎn)![]() 在拋物線上,且
在拋物線上,且![]() ,直線
,直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() ,
,![]() 與
與![]() 不重合),設(shè)直線
不重合),設(shè)直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .
.
(Ⅰ)求拋物線的方程;
(Ⅱ)當(dāng)![]() 時(shí),求證:直線
時(shí),求證:直線![]() 恒過(guò)定點(diǎn)并求出該定點(diǎn)的坐標(biāo).
恒過(guò)定點(diǎn)并求出該定點(diǎn)的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com