
【題目】經銷商小王對其所經營的某一型號二手汽車的使用年數![]() (0<
(0<![]() ≤10)與銷售價格
≤10)與銷售價格![]() (單位:萬元/輛)進行整理,得到如下的對應數據:
(單位:萬元/輛)進行整理,得到如下的對應數據:
使用年數 | 2 | 4 | 6 | 8 | 10 |
售價 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)試求![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(附:回歸方程![]() 中,
中,
(Ⅱ)已知每輛該型號汽車的收購價格為![]() 萬元,根據(Ⅰ)中所求的回歸方程,
萬元,根據(Ⅰ)中所求的回歸方程,
預測![]() 為何值時,小王銷售一輛該型號汽車所獲得的利潤
為何值時,小王銷售一輛該型號汽車所獲得的利潤![]() 最大.
最大.
科目:高中數學 來源: 題型:
【題目】已知正方形![]() 的邊長為
的邊長為![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起,使平面
折起,使平面![]() 平面
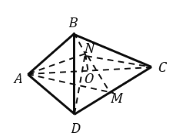
平面![]() ,得到如圖所示的三棱錐
,得到如圖所示的三棱錐![]() ,若
,若![]() 為
為![]() 邊的中點,
邊的中點,![]() 分別為
分別為![]() 上的動點(不包括端點),且
上的動點(不包括端點),且![]() ,設
,設![]() ,則三棱錐
,則三棱錐![]() 的體積取得最大值時,三棱錐
的體積取得最大值時,三棱錐![]() 的內切球的半徑為_______.
的內切球的半徑為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋擲一藍、一黃兩枚質地均勻的正四面體骰子,分別觀察底面上的數字.

(1)用表格表示試驗的所有可能結果;
(2)列舉下列事件包含的樣本點:A=“兩個數字相同”,B=“兩個數字之和等于5”,C=“藍色骰子的數字為2”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列說法是否正確,若錯誤,請舉出反例
(1)互斥的事件一定是對立事件,對立事件不一定是互斥事件;
(2)互斥的事件不一定是對立事件,對立事件一定是互斥事件;
(3)事件![]() 與事件B中至少有一個發生的概率一定比
與事件B中至少有一個發生的概率一定比![]() 與B中恰有一個發生的概率大;
與B中恰有一個發生的概率大;
(4)事件![]() 與事件B同時發生的概率一定比
與事件B同時發生的概率一定比![]() 與B中恰有一個發生的概率小.
與B中恰有一個發生的概率小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某顏料公司生產A,B兩種產品,其中生產每噸A產品,需要甲染料1噸,乙染料4噸,丙染料2噸,生產每噸B產品,需要甲染料1噸,乙染料0噸,丙染料5噸,且該公司一天之內甲、乙、丙三種染料的用量分別不超過50噸,160噸和200噸,如果A產品的利潤為300元/噸,B產品的利潤為200元/噸,設公司計劃一天內安排生產A產品x噸,B產品y噸.
(I)用x,y列出滿足條件的數學關系式,并在下面的坐標系中畫出相應的平面區域;
(II)該公司每天需生產A,B產品各多少噸可獲得最大利潤,最大利潤是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com