
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)記![]() ,
,![]() 是
是![]() 的導函數,如果
的導函數,如果![]() 是函數
是函數![]() 的兩個零點,且滿足
的兩個零點,且滿足![]() ,證明:
,證明:![]() .
.
【答案】(1)見解析(2)見解析
【解析】分析:(1)取出函數的導數,結合二次函數的性質,通過討論![]() 的范圍,求出函數的單調區間,即可;
的范圍,求出函數的單調區間,即可;
(2)求出 ,令
,令![]() ,則
,則![]() ,根據函數的單調性證明即可.
,根據函數的單調性證明即可.
詳解:(1)![]() 的定義域為
的定義域為![]() ,
,
![]() .
.
設![]() ,
,![]() 為二次函數,對稱軸
為二次函數,對稱軸![]() ,且恒過點
,且恒過點![]() ,
,
(i)當![]() 時,
時,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上單調遞減;
上單調遞減;
(ii)當![]() 時,
時,
令![]() ,可得
,可得![]() ,
,![]() .
.
若![]() 時,
時, ![]() .
.
當![]() 時,
時,![]() ,
,![]() ;
;![]() 時,
時,![]() .所以
.所以![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時,![]() ,.
,.
對任意![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() ,
,![]() .
.
當![]() 時,
時,![]() ,
,![]() ;
;![]() 時,
時,![]() ,
,![]() .
.
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
綜上,當![]() 時,
時,![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時, ![]() 在
在![]() 上單調遞減.
上單調遞減.
當![]() 時,
時,![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增.
上單調遞增.
(2)![]() ,
,![]() .
.
將![]()
兩式相減,整理得![]() ,
,
即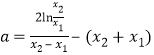 ,
,
所以![]()
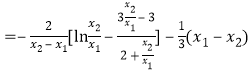
令![]() ,
,![]() ,
,
則![]() ,
,
所以![]() 在
在![]() 上單調遞減,故
上單調遞減,故![]()
又![]() ,所以
,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】經銷商小王對其所經營的某一型號二手汽車的使用年數![]() (0<
(0<![]() ≤10)與銷售價格
≤10)與銷售價格![]() (單位:萬元/輛)進行整理,得到如下的對應數據:
(單位:萬元/輛)進行整理,得到如下的對應數據:
使用年數 | 2 | 4 | 6 | 8 | 10 |
售價 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)試求![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(附:回歸方程![]() 中,
中,
(Ⅱ)已知每輛該型號汽車的收購價格為![]() 萬元,根據(Ⅰ)中所求的回歸方程,
萬元,根據(Ⅰ)中所求的回歸方程,
預測![]() 為何值時,小王銷售一輛該型號汽車所獲得的利潤
為何值時,小王銷售一輛該型號汽車所獲得的利潤![]() 最大.
最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四邊形EFGH為空間四邊形ABCD的一個截面,若截面為平行四邊形.
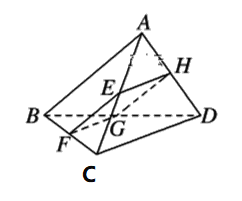
(1)求證:AB∥平面EFGH
(2)若AB=4,CD=6,求四邊形EFGH周長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,
,![]() 是圓上一動點,點
是圓上一動點,點![]() 在線段
在線段![]() 上,點
上,點![]() 在半徑
在半徑![]() 上,且滿足
上,且滿足![]() .
.
(1)當![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與軌跡
與軌跡![]() 交于點
交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線交
的直線交![]() 于點
于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,求點
,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心(![]() ,
,![]() )
)
C. 若該大學某女生身高增加1cm,則其體重約增加0.85kg
D. 若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,![]() ,
,![]() ,且
,且![]() ,E為PD中點.
,E為PD中點.

(I)求證:![]() 平面ABCD;
平面ABCD;
(II)求二面角B-AE-C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司共有60位員工,為提高員工的業務技術水平,公司擬聘請專業培訓機構進行培訓.培訓的總費用由兩部分組成:一部分是給每位參加員工支付400元的培訓材料費;另一部分是給培訓機構繳納的培訓費.若參加培訓的員工人數不超過30人,則每人收取培訓費1000元;若參加培訓的員工人數超過30人,則每超過1人,人均培訓費減少20元.設公司參加培訓的員工人數為x人,此次培訓的總費用為y元.
(1)求出y與x之間的函數關系式;
(2)請你預算:公司此次培訓的總費用最多需要多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com