【題目】已知在極坐標系中曲線
的極坐標方程為：
，以極點為坐標原點，以極軸為
軸的正半軸建立直角坐標系，曲線
的參數方程為：
(
為參數)，點
.
(1)求出曲線的直角坐標方程和曲線的普通方程；
(2)設曲線與曲線相交于
兩點，求
的值.
百年學典課時學練測系列答案科目：高中數學 來源： 題型：
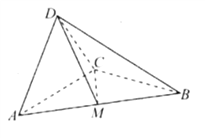
【題目】【2018江西撫州市高三八校聯考】如圖，在三棱錐
中， 
， 
， 
， 
，平面
平面
， 
為
的中點．
（I）求證： 
平面
；
（II）求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
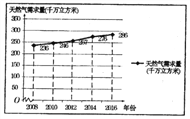
【題目】2017年12月，針對國內天然氣供應緊張的問題，某市政府及時安排部署，加氣站采取了緊急限氣措施，全市居民打響了節約能源的攻堅戰.某研究人員為了了解天然氣的需求狀況，對該地區某些年份天然氣需求量進行了統計，并繪制了相應的折線圖.
（Ⅰ）由折線圖可以看出，可用線性回歸模型擬合年度天然氣需求量
(單位：千萬立方米)與年份
(單位：年)之間的關系.并且已知關于的線性回歸方程是
，試確定
的值，并預測2018年該地區的天然氣需求量；
（Ⅱ）政府部門為節約能源出臺了《購置新能源汽車補貼方案》，該方案對新能源汽車的續航里程做出了嚴格規定，根據續航里程的不同，將補貼金額劃分為三類，A類：每車補貼1萬元，B類：每車補貼2.5萬元，C類：每車補貼3.4萬元.某出租車公司對該公司60輛新能源汽車的補貼情況進行了統計，結果如下表：
為了制定更合理的補貼方案，政府部門決定利用分層抽樣的方式了解出租車公司新能源汽車的補貼情況，在該出租車公司的60輛車中抽取6輛車作為樣本，再從6輛車中抽取2輛車進一步跟蹤調查，求恰好有1輛車享受3.4萬元補貼的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
： 
與拋物線
： 
相交于
， 
兩點，分別以點
， 
為切點作圓
的切線.若切線恰好都經過拋物線
的焦點
，則
（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】由題得設A
， 
，聯立圓E和拋物線得： 
，代入點A得
,又AF為圓的切線，故
，由拋物線得定義可知：AF=
，故
化簡得： 
，將點A代入圓得： 
，而
=
，故
故選A
點睛：此題幾何關系較為復雜，我們根據問題可知借此題關鍵為找到p和r的關系，我們可根據圓和拋物線相交結合拋物線的焦點弦長結論綜合計算可得其關系，從而求解
【題型】單選題
【結束】
12
【題目】已知函數
在點
處的切線為
，若直線
在
軸上的截距恒小于
，則實數
的取值范圍是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在等差數列
中，已知公差
， 
，且
， 
， 
成等比數列.
（1）求數列
的通項公式
；
（2）求
.
【答案】（1）
；（2）100
【解析】試題分析：（1）根據題意
， 
， 
成等比數列得
得
求出d即可得通項公式；（2）求項的絕對前n項和，首先分清數列有多少項正數項和負數項，然后正數項絕對值數值不變，負數項絕對值要變號，從而得
，得
，由
，得
，∴
計算 即可得出結論
解析：（1）由題意可得，則
， 
，
，即
，
化簡得
，解得
或
（舍去）.
∴
.
（2）由（1）得
時，
由
，得
，由
，得
，
∴
.
∴
.
點睛：對于數列第一問首先要熟悉等差和等比通項公式及其性質即可輕松解決，對于第二問前n項的絕對值的和問題，首先要找到數列由多少正數項和負數項，進而找到絕對值所影響的項，然后在求解即可得結論
【題型】解答題
【結束】
18
【題目】甲、乙兩家銷售公司擬各招聘一名產品推銷員，日工資方案如下: 甲公司規定底薪80元，每銷售一件產品提成1元; 乙公司規定底薪120元，日銷售量不超過45件沒有提成，超過45件的部分每件提成8元.
(I)請將兩家公司各一名推銷員的日工資
(單位: 元) 分別表示為日銷售件數
的函數關系式;
(II)從兩家公司各隨機選取一名推銷員，對他們過去100天的銷售情況進行統計，得到如下條形圖。若記甲公司該推銷員的日工資為
,乙公司該推銷員的日工資為
(單位: 元)，將該頻率視為概率，請回答下面問題:
某大學畢業生擬到兩家公司中的一家應聘推銷員工作，如果僅從日均收入的角度考慮，請你利用所學的統計學知識為他作出選擇，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖3，
是一個直角梯形，
，
為
邊上一點，
、
相交于
，
，
，
．將△
沿折起，使平面⊥平面
，連接、，得到如圖4所示的四棱錐
．
（Ⅰ）求證：
⊥平面
；
（Ⅱ）求直線
與面
所成角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知在平面直角坐標系
中的一個橢圓，它的中心在原點，左焦點為
，右頂點為
，設點
.
（1）求該橢圓的標準方程；
（2）若
是橢圓上的動點，求線段
中點
的軌跡方程；
（3）過原點
的直線交橢圓于點
，求
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
