
【題目】已知拋物線![]() 上一點
上一點![]() 到焦點F的距離為
到焦點F的距離為![]() .
.
(1)求拋物線M的方程;
(2)過點F斜率為k的直線l與M相交于C,D兩點,線段![]() 的垂直平分線
的垂直平分線![]() 與M相交于
與M相交于![]() 兩點,點
兩點,點![]() 分別為線段
分別為線段![]() 和
和![]() 的中點.
的中點.
①試用k表示點![]() 的坐標;
的坐標;
②若以線段![]() 為直徑的圓過點C,求直線l的方程.
為直徑的圓過點C,求直線l的方程.
【答案】(1)![]() (2)①
(2)①![]() ;
;![]() ②
②![]() ,或
,或![]()
【解析】
(1)根據(jù)題意可得![]() 且
且![]() ,解得
,解得![]() ,進而得出拋物線方程.
,進而得出拋物線方程.
(2)①點![]() 的坐標為
的坐標為![]() ,寫出直線
,寫出直線![]() 的方程為:
的方程為:![]() ,聯(lián)立直線
,聯(lián)立直線![]() 與拋物線
與拋物線![]() 的方程得
的方程得![]()
![]() ,設
,設![]() ,
,![]() ,
,![]() ,
,![]() ,則由韋達定理得
,則由韋達定理得![]() ,
,![]() ,進而得中點
,進而得中點![]() 的坐標,再寫出線段
的坐標,再寫出線段![]() 垂直平分線
垂直平分線![]() 的方程:
的方程:![]() ,聯(lián)立它與拋物線方程,同理得線段
,聯(lián)立它與拋物線方程,同理得線段![]() 中點
中點![]() 的坐標.
的坐標.
②根據(jù)題意得![]() ,
,![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() ,即
,即![]() ,分別由拋物線定義,弦長公式,兩點之間得距離公式表示
,分別由拋物線定義,弦長公式,兩點之間得距離公式表示![]() ,
,![]() ,
,![]() ,代入化簡解得
,代入化簡解得![]() ,進而得直線
,進而得直線![]() 的方程.
的方程.
解:(1)根據(jù)拋物線的定義和已知條件,得![]() ,故
,故![]() ,
,
由點Q在M上,可知![]() ,把
,把![]() 代入,得
代入,得![]() .
.
所以拋物線M的方程為:![]() .
.
(2)①由(1)可知點F的坐標為![]() ,所以直線l的方程為:
,所以直線l的方程為:![]() .
.
聯(lián)立![]() 消去y得
消去y得![]() ,
,
設![]() ,則
,則![]() ,所以
,所以![]() ,
,
所以線段![]() 中點
中點![]() .
.
因為![]() 過點E且與l垂直,所以
過點E且與l垂直,所以![]() 的方程為:
的方程為:![]()
聯(lián)立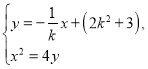 消去y,得
消去y,得![]() ,
,![]() 顯然成立.
顯然成立.
設![]() ,則
,則![]() ,所以
,所以![]() ,
,
所以線段![]() 中點
中點![]()
②因為以線段![]() 為直徑的圓過點C,所以
為直徑的圓過點C,所以![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() .
.
根據(jù)拋物線定義,得![]() ,
,
又![]()
![]() ,
,
![]() ,
,
所以,由![]() ,
,
得![]() ,
,
解方程得![]() ,所以直線l的方程為
,所以直線l的方程為![]() ,或
,或![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線C:![]() 的焦點為F,直線y=4與y軸的交點為P,與C的交點為Q,且
的焦點為F,直線y=4與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求拋物線C的方程;
(2)過F的直線l與C相交于A,B兩點,若AB的垂直平分線![]() 與C相交于M,N兩點,且A,M,B,N四點在同一個圓上,求直線l的方程.
與C相交于M,N兩點,且A,M,B,N四點在同一個圓上,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某段城鐵線路上依次有![]() 、
、![]() 、
、![]() 三站,
三站,![]() ,
,![]() ,在列車運行時刻表上,規(guī)定列車
,在列車運行時刻表上,規(guī)定列車![]() 時整從
時整從![]() 站出發(fā),
站出發(fā),![]() 時
時![]() 分到達
分到達![]() 站并停車
站并停車![]() ,
,![]() 時
時![]() 分到達
分到達![]() 站,在實際運行時,假設列車從
站,在實際運行時,假設列車從![]() 站正點出發(fā),在
站正點出發(fā),在![]() 站停留
站停留![]() ,并在行駛時以同一速度
,并在行駛時以同一速度![]() 勻速行駛,列車從
勻速行駛,列車從![]() 站到達某站的時間與時刻表上相應時間之差的絕對值稱為列車在該站的運行誤差.
站到達某站的時間與時刻表上相應時間之差的絕對值稱為列車在該站的運行誤差.
(1)分別寫出列車在![]() 、
、![]() 兩站的運行誤差;
兩站的運行誤差;
(2)若要求列車在![]() 、
、![]() 兩站的運行誤差之和不超過
兩站的運行誤差之和不超過![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)若函數(shù)![]() 有兩個極值點
有兩個極值點![]() 且
且![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在氣象臺![]() 正南方向
正南方向![]() 處有一臺風中心,它以
處有一臺風中心,它以![]() 的速度向北偏東
的速度向北偏東![]() 方向移動,距臺風中心
方向移動,距臺風中心![]() 以內(nèi)的地方都要受其影響.問:從現(xiàn)在起,大約多長時間后,氣象臺
以內(nèi)的地方都要受其影響.問:從現(xiàn)在起,大約多長時間后,氣象臺![]() 所在地將遭受臺風影響?持續(xù)多長時間?(
所在地將遭受臺風影響?持續(xù)多長時間?(![]() ,
,![]() ,結(jié)果精確到0.01)
,結(jié)果精確到0.01)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】全民健身旨在全面提高國民體質(zhì)和健康水平,倡導全民做到每天參加一次以上的健身活動,學會兩種以上健身方法,每年進行一次體質(zhì)測定.為響應全民健身號召,某單位在職工體測后就某項健康指數(shù)(百分制)隨機抽取了30名職工的體測數(shù)據(jù)作為樣本進行調(diào)查,具體數(shù)據(jù)如莖葉圖所示,其中有1名女職工的健康指數(shù)的數(shù)據(jù)模糊不清(用x表示),已知這30名職工的健康指數(shù)的平均數(shù)為76.2.
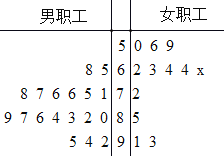
(1)根據(jù)莖葉圖,求樣本中男職工健康指數(shù)的眾數(shù)和中位數(shù);
(2)根據(jù)莖葉圖,按男女用分層抽樣從這30名職工中隨機抽取5人,再從抽取的5人中隨機抽取2人,求抽取的2人都是男職工的概率;
(3)經(jīng)計算,樣本中男職工健康指數(shù)的平均數(shù)為81,女職工現(xiàn)有數(shù)據(jù)(即剔除x)健康指數(shù)的平均數(shù)為69,方差為190,求樣本中所有女職工的健康指數(shù)的平均數(shù)和方差(結(jié)果精確到0.1).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了預防流感,某學校對教室用藥熏消毒法進行消毒,已知藥物釋放過程中,室內(nèi)每立方米空氣中的含藥量![]() 與時間
與時間![]() 成正比,藥物釋放完畢后,
成正比,藥物釋放完畢后,![]() 與
與![]() 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為![]() (
(![]() 為常數(shù)).如圖所示,根據(jù)圖中提供的信息,回答下列問題:
為常數(shù)).如圖所示,根據(jù)圖中提供的信息,回答下列問題:
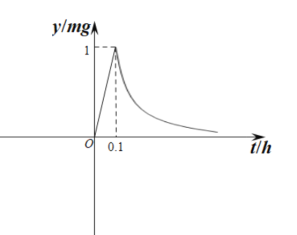
(1)從藥物釋放開始,每立方米空氣中的含藥量![]() 與時間
與時間![]() 之間的函數(shù)關(guān)系式為________;
之間的函數(shù)關(guān)系式為________;
(2)據(jù)測定,當空氣中每立方米的含藥量降低到![]() 以下時,學生方可進教室,那么從藥物釋放開始,至少需要經(jīng)過多少時間學生才能回到教室?
以下時,學生方可進教室,那么從藥物釋放開始,至少需要經(jīng)過多少時間學生才能回到教室?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 和圓
和圓![]() ,傾斜角為45°的直線
,傾斜角為45°的直線![]() 過拋物線
過拋物線![]() 的焦點,且
的焦點,且![]() 與圓
與圓![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)動點![]() 在拋物線
在拋物線![]() 的準線上,動點
的準線上,動點![]() 在
在![]() 上,若
上,若![]() 在
在![]() 點處的切線
點處的切線![]() 交
交![]() 軸于點
軸于點![]() ,設
,設![]() .求證點
.求證點![]() 在定直線上,并求該定直線的方程.
在定直線上,并求該定直線的方程.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com