
【題目】函數f(x)=a![]() -2ln x(a∈R).
-2ln x(a∈R).
(Ⅰ)當a=2時,求曲線f(x)在x=2處的切線方程;
(Ⅱ)若a>![]() ,且m,n分別為f(x)的極大值和極小值,S=m-n,求證:S<
,且m,n分別為f(x)的極大值和極小值,S=m-n,求證:S<![]() .
.
【答案】(Ⅰ)3x-2y-4ln 2=0(Ⅱ)見解析
【解析】試題分析:(Ⅰ) 求出導數,計算![]() 可得到切線斜率,求出
可得到切線斜率,求出![]() 可得切點坐標,利用點斜式即可求出切線方程;(Ⅱ) 設
可得切點坐標,利用點斜式即可求出切線方程;(Ⅱ) 設![]() 的兩根為
的兩根為![]() ,所以
,所以![]() ,求出
,求出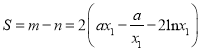 ,將
,將![]() 的值代入
的值代入![]() 的解析式,化簡,構造新函數
的解析式,化簡,構造新函數![]() ,求導數,利用導數研究函數的單調性,應用單調性求最值,即可證明結論.
,求導數,利用導數研究函數的單調性,應用單調性求最值,即可證明結論.
試題解析:(Ⅰ) f′(x)=a+![]() -
-![]() ,若a=2,則f′(2)=2+
,若a=2,則f′(2)=2+![]() -
-![]() =
=![]() ,f(2)=4-1-2ln 2=3-2ln 2,則曲線f(x)在x=2處的切線方程為y-(3-2ln 2)=
,f(2)=4-1-2ln 2=3-2ln 2,則曲線f(x)在x=2處的切線方程為y-(3-2ln 2)=![]() (x-2),化簡得3x-2y-4ln 2=0.
(x-2),化簡得3x-2y-4ln 2=0.
(Ⅱ)f′(x)=![]() ,令f′(x)=0,得ax2-2x+a=0,
,令f′(x)=0,得ax2-2x+a=0,
則Δ>0且![]() <a,得
<a,得![]() <a<1,此時設f′(x)=0的兩根為x1,x2(x1<x2),
<a<1,此時設f′(x)=0的兩根為x1,x2(x1<x2),
所以m=f(x1),n=f(x2).
因為x1x2=1,所以x1<1<x2,由![]() <a<1,
<a<1,
所以S=m-n=ax1-![]() -2ln x1-(ax2-
-2ln x1-(ax2-![]() -2ln x2)
-2ln x2)
=ax1-![]() -2ln x1-(
-2ln x1-(![]() -ax1+2ln x1)
-ax1+2ln x1)
=2(ax1-![]() -2ln x1).
-2ln x1).
由a![]() -2x1+a=0得a=
-2x1+a=0得a=![]() ,
,
代入上式得S=4(![]() -lnx1)
-lnx1)
=4(![]() -
-![]() ln
ln![]() ).
).
令h(x)=ax2-2x+a,則h![]() =
=![]() -
-![]() +a
+a
=a·![]() -
-![]() >
>![]() ·
·![]() -
-![]() =
=![]() -
-![]() =0,
=0,
x=![]()
![]() 是拋物線h(x)的對稱軸.
是拋物線h(x)的對稱軸.
∴![]() <x1<1.
<x1<1.
令![]() =t,所以
=t,所以![]() <t<1,g(x)=
<t<1,g(x)=![]() -
-![]() ln x,則S=4g(t),
ln x,則S=4g(t),
g'(x)=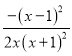 <0,所以g(x)在
<0,所以g(x)在![]() ≤x≤1上為減函數,
≤x≤1上為減函數,
從而g(1)<g(t)<g(![]() ),即0<g(t)<
),即0<g(t)< ![]() ,所以S<
,所以S<![]() .
.
【方法點晴】本題主要考查利用導數求曲線切線方程以及利用導數研究函數的單調性與極值,屬于難題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數,即
處的導數,即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數不存在,切線方程為
軸平行時,在 處導數不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,f(x+1)為奇函數,f(0)=0,當x∈(0,1]時,f(x)=log2x,則在區間(8,9)內滿足方程f(x)+2=![]() 的實數x為( )
的實數x為( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量a=(sin x,mcos x),b=(3,-1).
(1)若a∥b,且m=1,求2sin2x-3cos2x的值;
(2)若函數f(x)=a·b的圖象關于直線![]() 對稱,求函數f(2x)在
對稱,求函數f(2x)在![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
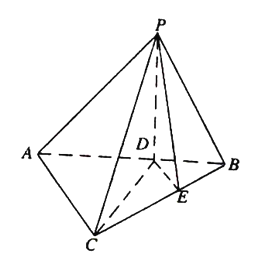
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為線段
分別為線段![]() 上的點,且
上的點,且![]() ,
, ![]() ,
, ![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角.
所成的銳二面角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線M的參數方程為![]() (θ為參數),若以直角坐標系的原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線N的極坐標方程為ρsin(θ+
(θ為參數),若以直角坐標系的原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線N的極坐標方程為ρsin(θ+![]() )=
)=![]() t(其中t為常數).
t(其中t為常數).
(Ⅰ)若曲線N與曲線M只有一個公共點,求t的值;
(Ⅱ)當t=-1時,求曲線M上的點與曲線N上的點的最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=![]() ,D,E分別是AC1,BB1的中點,則直線DE與平面BB1C1C所成角的正弦值為________.
,D,E分別是AC1,BB1的中點,則直線DE與平面BB1C1C所成角的正弦值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別是a,b,c,且2acosA=bcosC+ccosB.
(Ⅰ)求A的大小;
(Ⅱ)若a=2,求b+c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+![]() +2(m為實常數).
+2(m為實常數).
(1)若函數f(x)圖象上動點P到定點Q(0,2)的距離的最小值為![]() ,求實數m的值;
,求實數m的值;
(2)若函數y=f(x)在區間[2,+∞)上是增函數,試用函數單調性的定義求實數m的取值范圍;
(3)設m<0,若不等式f(x)≤kx在x∈[![]() ,1]時有解,求k的取值范圍.
,1]時有解,求k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com