
【題目】在平面直角坐標系xOy中,已知圓C:x2+y2=4和直線l:x=4,M為l上一動點,A1 , A2為圓C與x軸的兩個交點,直線MA1 , MA2與圓C的另一個交點分別為P、Q.
(1)若M點的坐標為(4,2),求直線PQ方程;
(2)求證直線PQ過定點,并求出此定點的坐標.
【答案】
(1)解:當M(4,2),
則A1(﹣2,0),A2(2,0).
直線MA1的方程:x﹣3y+2=0,
解 ![]() 得
得 ![]() .
.
直線MA2的方程:x﹣y﹣2=0,
解 ![]() 得Q(0,﹣2),
得Q(0,﹣2),
由兩點式可得直線PQ的方程為2x﹣y﹣2=0
(2)證明:設M(4,t),則直線MA1的方程: ![]() ,直線MA2的方程:
,直線MA2的方程: ![]()
由 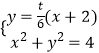 得
得 ![]()
由 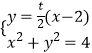 得
得 ![]()
當 ![]() 時,
時, ![]() ,
,
則直線PQ: ![]()
化簡得 ![]() ,恒過定點(1,0)
,恒過定點(1,0)
當 ![]() 時,
時, ![]() ,直線PQ:x=1,恒過定點(1,0)
,直線PQ:x=1,恒過定點(1,0)
故直線PQ過定點(1,0)
【解析】(1)求出A1 , A2的坐標,可求直線MA1的方程、直線MA2的方程,與圓的方程聯立,求出P,Q的坐標,由兩點式求直線PQ方程;(2)設M(4,t),則直線MA1的方程: ![]() ,直線MA2的方程:
,直線MA2的方程: ![]() ,分別代入圓的方程,求出P,Q的坐標,分類討論,確定直線PQ的方程,即可得出結論.
,分別代入圓的方程,求出P,Q的坐標,分類討論,確定直線PQ的方程,即可得出結論.


 互動英語系列答案
互動英語系列答案科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
(1)求cos(α﹣β)的值;
(2)若0<α< ![]() ,﹣
,﹣ ![]() <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
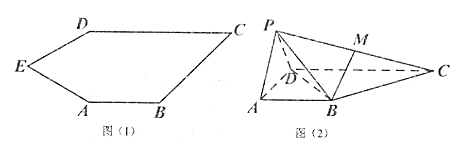
【題目】如圖(1)五邊形![]() 中,
中, ![]()
![]() ,將
,將![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() ,如圖(2),點
,如圖(2),點![]() 為線段
為線段![]() 的中點,且
的中點,且![]() 平面
平面![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的體積為
的體積為![]() ,求四面體
,求四面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在[﹣1,1]上的奇函數,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判斷f(x)的單調性,并加以證明;
(2)解不等式 ![]() ;
;
(3)若f(x)≤m2﹣2am+1對所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com