【題目】已知定義在
上的函數
的圖像是一條連續不斷的曲線，且在任意區間上都不是常值函數.設
，其中分點
將區間
任意劃分成
個小區間
，記
，稱為關于區間的
階劃分“落差總和”.
當
取得最大值且取得最小值
時，稱存在“最佳劃分”
.
(1)已知
，求
的最大值
；
(2)已知
，求證：在上存在“最佳劃分”
的充要條件是在上單調遞增.
(3)若是偶函數且存在“最佳劃分”
，求證：是偶數，且
.
【答案】(1)3；(2)見解析；(3)見解析
【解析】
(1)直接利用題中給的定義求解即可；
(2)利用函數的單調性和數列的信息應用求出充要條件；
(3)利用函數的奇偶性和存在的最佳劃分，進一步建立函數的單調區間，最后求出函數的關系式.
(1)
；
(2)若
在
上單調遞增，則
，
故在上存在“最佳劃分”
若在上存在“最佳劃分”，倘若在上不單調遞增，
則存在
.
由
（*）
等號當且僅當
時取得，此時
，與題設矛盾，舍去，故（*）式中等號不成立，即：增加分點
后，“落差總和”會增加，故
取最大值時
的最小值大于1，與條件矛盾.
所以在上單調遞增；
(3)由(2)的證明過程可知，在任間區間上，若存在最佳劃分
，則當
時，為常值函數（舍）；當
時，單調遞增；當
時，單調遞減，
若在上存在最佳劃分
，則此時在每個小區間
上均為最佳劃分
.否則，添加分點后可使在上的“落差總和”增大，從而不是“落差總和”的最大值，與“在上存在最佳劃分”矛盾，故在每個小區間上都是單調，
若在上存在最佳劃分，則在相鄰的兩個區間
上具有不同的單調性，否則，
，
減少分點
，“落差總和”的值不變，而的值減少1，故的最小值不是
，與“在上存在最佳劃分”矛盾，
存在“最佳劃分”
，故在每個小區間上都單調，而是偶函數，故在
軸兩側的單調區間對稱，共有偶數個單調區間，且當
時，
，從而有
.
科目：高中數學 來源： 題型：
【題目】某單位共有老年人120人，中年人360人，青年人n人，為調查身體健康狀況，需要從中抽取一個容量為m的樣本，用分層抽樣的方法進行抽樣調查，樣本中的中年人為6人，則n和m的值不可以是下列四個選項中的哪組( )
A.n=360，m=14B.n=420，m=15C.n=540，m=18D.n=660，m=19
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，共享單車已經悄然進入了廣大市民的日常生活，并慢慢改變了人們的出行方式.為了更好地服務民眾，某共享單車公司在其官方
中設置了用戶評價反饋系統，以了解用戶對車輛狀況和優惠活動的評價，現從評價系統中選出
條較為詳細的評價信息進行統計，車輛狀況和優惠活動評價的
列聯表如下:
對優惠活動好評 | 對優惠活動不滿意 | 合計 | |
對車輛狀況好評 |
|
|
|
對車輛狀況不滿意 |
|
|
|
合計 |
|
|
|
(1)能否在犯錯誤的概率不超過
的前提下認為優惠活動好評與車輛狀況好評之間有關系?
(2)為了回饋用戶，公司通過向用戶隨機派送騎行券，用戶可以將騎行券用于騎行付費，也可以通過轉贈給好友某用戶共獲得了
張騎行券，其中只有
張是一元券現該用戶從這張騎行券中隨機選取張轉贈給好友，求選取的張中至少有
張是一元券的概率.
附:下面的臨界值表僅供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式: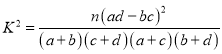
，其中
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】心理學研究表明，人極易受情緒的影響，某選手參加7局4勝制的兵乒球比賽.
（1）在不受情緒的影響下，該選手每局獲勝的概率為
；但實際上，如果前一句獲勝的話，此選手該局獲勝的概率可提升到
；而如果前一局失利的話，此選手該局獲勝的概率則降為
，求該選手在前3局獲勝局數
的分布列及數學期望；
（2）假設選手的三局比賽結果互不影響，且三局比賽獲勝的概率為
，記
為銳角
的內角，求證：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
的極坐標方程為
，曲線
的參數方程為
（
為參數）.
（1）求直線的直角坐標方程和曲線的普通方程；
（2）若過
且與直線垂直的直線
與曲線相交于
、
兩點，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C的對邊分別為a，b，c，且sin2A+sin2B+sin2C＝sinAsinB+sinBsinC+sinCsin A．
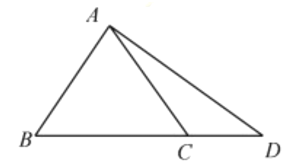
（1）證明：△ABC是正三角形；
（2）如圖，點D在邊BC的延長線上，且BC＝2CD，AD
，求sin∠BAD的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
