Question

【題目】已知橢圓的長軸長是焦距的2倍，且過點．

（1）求橢圓C的方程；

（2）設為橢圓C上的動點，F為橢圓C的右焦點，A、B分別為橢圓C的左、右頂點，點滿足．

①證明：為定值；

②設Q是直線上的動點，直線AQ、BQ分別另交橢圓C于M、N兩點，求的最小值．

Answer 1

【答案】（1）（2）①見解析②3

【解析】

（1）由題意可得又過一點，及，，之間的關系求出，，進而求出橢圓的方程；

（2）①由（1）可得右焦點，，的坐標，求出向量的模，及向量的模可證得為定值；

②由題意方程可得為右準線，設的坐標，求出直線，的直線與橢圓聯立求出，的橫坐標，再由橢圓的性質到焦點的距離與到準線的距離的比為離心率可得用，的橫坐標表示，由均值不等式可得其最小值.

解：（1）由題意可得，，，

解得：，，

所以橢圓的方程為：；

（2）由（1）可得，，，

①因為為橢圓C上的動點，

點滿足，所以；

所以

，

所以：，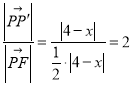

所以可證為定值2．

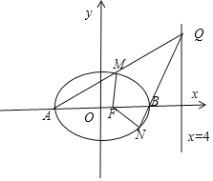
②由題意設，所以，

所以直線的方程為：，

聯立直線與橢圓的方程：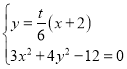

整理可得：，

所以，所以，

同理，所以直線的方程：，

整理可得：，

所以，所以，

因為為右準線，

所以由到焦點的距離與到準線的距離的比為離心率，

可得：

，

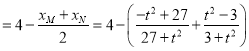
當且僅當，即時取等號．

所以的最小值為3．