
【題目】設函數 ![]() ,其中[x]表示不超過x的最大整數,若直線y=kx+k(k>0)與函數y=f(x)的圖象恰有三個不同的交點,則k的取值范圍是 .
,其中[x]表示不超過x的最大整數,若直線y=kx+k(k>0)與函數y=f(x)的圖象恰有三個不同的交點,則k的取值范圍是 .
【答案】[ ![]() ,
, ![]() )
)
【解析】解:∵函數 ![]() , ∴函數的圖象如下圖所示:
, ∴函數的圖象如下圖所示: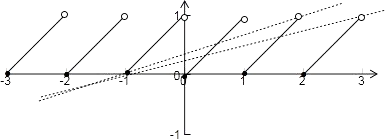
∵y=kx+k=k(x+1),故函數圖象一定過(﹣1,0)點
若f(x)=kx+k有三個不同的根,
則y=kx+k與y=f(x)的圖象有三個交點
當y=kx+k過(2,1)點時,k= ![]() ,
,
當y=kx+k過(3,1)點時,k= ![]() ,
,
故f(x)=kx+k有三個不同的根,則實數k的取值范圍是[ ![]() ,
, ![]() )
)
【考點精析】解答此題的關鍵在于理解函數的零點與方程根的關系的相關知識,掌握二次函數的零點:(1)△>0,方程 有兩不等實根,二次函數的圖象與 軸有兩個交點,二次函數有兩個零點;(2)△=0,方程 有兩相等實根(二重根),二次函數的圖象與 軸有一個交點,二次函數有一個二重零點或二階零點;(3)△<0,方程 無實根,二次函數的圖象與 軸無交點,二次函數無零點.


科目:高中數學 來源: 題型:
【題目】一個函數f(x),如果對任意一個三角形,只要它的三邊長a,b,c都在f(x)的定義域內,就有f(a),f(b),f(c)也是某個三角形的三邊長,則稱f(x)為“三角保型函數”,給出下列函數: ①f(x)= ![]() ;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
其中是“三角保型函數”的是( )
A.①②
B.①③
C.②③④
D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為R,它的導函數y=f′(x)的部分圖象如圖所示,則下面結論正確的是( ) 
A.在(1,2)上函數f(x)為增函數
B.在(3,4)上函數f(x)為減函數
C.在(1,3)上函數f(x)有極大值
D.x=3是函數f(x)在區間[1,5]上的極小值點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() ,g(x)=2ln(x+m).
,g(x)=2ln(x+m).
(1)當m=0,存在x0∈[ ![]() ,e](e為自然對數的底數),使
,e](e為自然對數的底數),使 ![]() ,求實數a的取值范圍;
,求實數a的取值范圍;
(2)當a=m=1時,設H(x)=xf(x)+g(x),在H(x)的圖象上是否存在不同的兩點A(x1 , y1),B(x2 , y2)(x1>x2>﹣1),使得H(x1)﹣H(x2)= ![]() ?請說明理由.
?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】偶函數y=f(x)在區間(﹣∞,﹣1]上是增函數,則下列不等式成立的是( )
A.f(﹣1)>f( ![]() )
)
B.f( ![]() )>f(﹣
)>f(﹣ ![]() )??
)??
C.f(4)>f(3)
D.f(﹣ ![]() )>f(
)>f( ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一條筆直公路上有A,B兩地,甲騎自行車從A地到B地,乙騎著摩托車從B地到A地,到達A地后立即按原路返回,如圖是甲乙兩人離A地的距離![]() 與行駛時間
與行駛時間![]() 之間的函數圖象,根據圖象解答以下問題:
之間的函數圖象,根據圖象解答以下問題:
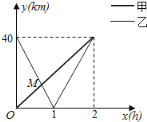
![]() 直接寫出
直接寫出![]() ,
,![]() 與x之間的函數關系式
與x之間的函數關系式![]() 不必寫過程
不必寫過程![]() ,求出點M的坐標,并解釋該點坐標所表示的實際意義;
,求出點M的坐標,并解釋該點坐標所表示的實際意義;
![]() 若兩人之間的距離不超過5km時,能夠用無線對講機保持聯系,求在乙返回過程中有多少分鐘甲乙兩人能夠用無線對講機保持聯系;
若兩人之間的距離不超過5km時,能夠用無線對講機保持聯系,求在乙返回過程中有多少分鐘甲乙兩人能夠用無線對講機保持聯系;
![]() 若甲乙兩人離A地的距離之積為
若甲乙兩人離A地的距離之積為![]() ,求出函數
,求出函數![]() 的表達式,并求出它的最大值.
的表達式,并求出它的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四人進行選擇題解題比賽,已知每個選擇題選擇正確得![]() 分,否則得
分,否則得![]() 分.其測試結果如下:甲解題正確的個數小于乙解題正確的個數,乙解題正確的個數小于丙解題正確的個數,丙解題正確的個數小于丁解題正確的個數;且丁解題正確的個數的
分.其測試結果如下:甲解題正確的個數小于乙解題正確的個數,乙解題正確的個數小于丙解題正確的個數,丙解題正確的個數小于丁解題正確的個數;且丁解題正確的個數的![]() 倍小于甲解題正確的個數的
倍小于甲解題正確的個數的![]() 倍,則這四人測試總得分數最少為( )
倍,則這四人測試總得分數最少為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為考察某種藥物預防疾病的效果,進行動物試驗,調查了 105 個樣本,統計結果為:服藥的共有 55 個樣本,服藥但患病的仍有 10 個樣本,沒有服藥且未患病的有 30個樣本.
(1)根據所給樣本數據完成 ![]() 列聯表中的數據;
列聯表中的數據;
(2)請問能有多大把握認為藥物有效?
(參考公式:![]() 獨立性檢驗臨界值表
獨立性檢驗臨界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合計 | |
服藥 | |||
沒服藥 | |||
合計 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com