Question

【題目】若實數滿足，則稱為函數的不動點．

（1）求函數的不動點；

（2）設函數，其中為實數．

① 若時，存在一個實數，使得既是的不動點，又是 的不動點（是函數的導函數），求實數的取值范圍；

② 令，若存在實數，使，，， 成各項都為正數的等比數列，求證：函數存在不動點．

Answer 1

【答案】（1）函數的不動點為；（2）①，②見解析.

【解析】試題分析：

(1)結合函數的單調性可得函數的不動點為;

(2)由題意得到方程組，消去c可得實數的取值范圍是，

(3)滿足題意時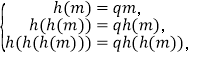結合導函數與原函數的性質討論計算即可證得結論.

試題解析：

（1）由題意可知，．

令，．故．

列表：

x		1
		0
		極大值

所以，方程有唯一解．

所以函數的不動點為．

（2）① 由題意可知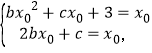

消去，得，，所以．

② ．

由題意知，，，成各項都為正數的等比數列，

故可設公比為，則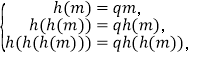

故方程有三個根，，．

又因為，所以為二次函數，

故方程為二次方程，最多有兩個不等的根．則，，中至少有兩個值相等．

當時，方程有實數根，也即函數存在不動點，符合題意；

當時，則，，故，又因為各項均為正數，則，也即，同上，函數存在不動點，符合題意；

當時，則，，同上，函數存在不動點，符合題意；

綜上所述，函數存在不動點．