【題目】某項競賽分為初賽、復賽、決賽三個階段進行，每個階段選手要回答一個問題．規定正確回答問題者進入下一階段競賽，否則即遭淘汰．已知某選手通過初賽、復賽、決賽的概率分別是
且各階段通過與否相互獨立．
(1)求該選手在復賽階段被淘汰的概率；
(2)設該選手在競賽中回答問題的個數為ξ，求ξ的分布列與均值．
【答案】(1) 
(2) ξ的分布列為：
ξ | 1 | 2 | 3 |
P |
|
|
|
Eξ=2
【解析】試題分析：（1）選手在復賽階段被淘汰的概率P=P（A 
），分別求出P（A）=
，P（B）= 
，代入公式P=P（A 
）=P（A）P（
）得到結果。（2）根據題意得到P（ξ=1）= 
，P（ξ=2）= 
，P（ξ=3）=
，再根據期望公式得到結果。
解析：
（1）解：記“該選手通過初賽”為事件A，“該選手通過復賽”為事件B，“該選手通過決賽”為事件C，則P（A）=
，P（B）= 
，P（C）=
那么該選手在復賽階段被淘汰的概率P=P（A 
）=P（A）P（
）= 
（2）解：ξ可能取值為1，2，3．
P（ξ=1）=1﹣
= 
，
P（ξ=2）= 
P（ξ=3）= 
+
=
故ξ的分布列為：
ξ | 1 | 2 | 3 |
P |
|
|
|
Eξ=1
+2
+3
=2
七彩題卡口算應用一點通系列答案科目：高中數學 來源： 題型：
【題目】已知數列{an}是等差數列，a10＝4a3，a4＝3a1＋7.
(1)求通項公式an；
(2)若bn＝an－2an＋2，求數列{bn}的前n項和Sn.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4—4：坐標系與參數方程
在直角坐標系
中，直線
的參數方程為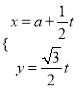
．以坐標原點為極點，以
軸的正半軸為極軸，建立極坐標系，曲線
的極坐標方程為
．
（Ⅰ）寫出
的普通方程和
的直角坐標方程；
（Ⅱ）設直線
與曲線
交于A,B兩點，當
時，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856264)
已知函數f(x)＝aln x，e為自然對數的底數．
(Ⅰ)曲線f(x)在點A(1，f(1))處的切線與坐標軸所圍成的三角形的面積為2，求實數a的值；
(Ⅱ)若f(x)≥1－
恒成立，求實數a的值取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2017·河西五市二聯)下列說法正確的是( )
A. 命題“x∈R，ex＞0”的否定是“x∈R，ex＞0”
B. 命題“已知x，y∈R，若x＋y≠3，則x≠2或y≠1”是真命題
C. “x2＋2x≥ax在x∈[1,2]上恒成立”“(x2＋2x)min≥(ax)min在x∈[1,2]上恒成立”
D. 命題“若a＝－1，則函數f(x)＝ax2＋2x－1只有一個零點”的逆命題為真命題
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠生產某種產品的年固定成本為250萬元，每生產x千件，需另投入成本為C（x）萬元，當年產量不足80千件時，C（x）＝
x2＋10x（萬元）；當年產量不少于80千件時，C（x）＝51x＋
－1 450（萬元）．通過市場分析，若每件售價為500元時，該廠年內生產的商品能全部銷售完．
（1）寫出年利潤L（萬元）關于年產量x（千件）的函數解析式；
（2）年產量為多少千件時，該廠在這一商品的生產中所獲利潤最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2018屆吉林省普通中學高三第二次調研】某校冬令營有三名男同學A,B,C和三名女同學X,Y,Z，
（1）從6人中抽取2人參加知識競賽，求抽取的2人都是男生的概率；
（2）若從這3名男生和3名女生中各任選一名，求這2人中包含A且不包含X的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
