
【題目】選修4﹣4:坐標系與參數方程 曲線C1的參數方程為 ![]() (α為參數),在以原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C2的極坐標方程為ρcos2θ=sinθ.
(α為參數),在以原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C2的極坐標方程為ρcos2θ=sinθ.
(1)求曲線C1的極坐標方程和曲線C2的直角坐標方程;
(2)若射線l:y=kx(x≥0)與曲線C1 , C2的交點分別為A,B(A,B異于原點),當斜率k∈(1, ![]() ]時,求|OA||OB|的取值范圍.
]時,求|OA||OB|的取值范圍.
【答案】
(1)解:曲線C1的直角坐標方程為(x﹣1)2+y2=1,即x2+y2﹣2x=0,
∴曲線C1的極坐標方程為ρ2﹣2ρcosθ=0,即ρ=2cosθ.
∵曲線C2的極坐標方程為ρcos2θ=sinθ,即ρ2cos2θ=ρsinθ,
∴曲線C2的直角坐標方程為x2=y
(2)解:設射線l的傾斜角為α,
則射線l的參數方程為 ![]() (t為參數,
(t為參數, ![]() ).
).
把射線l的參數方程代入曲線C1的普通方程得:t2﹣2tcosα=0,
解得t1=0,t2=2cosα.
∴|OA|=|t2|=2cosα.
把射線l的參數方程代入曲線C2的普通方程得:cos2αt2=tsinα,
解得t1=0,t2= ![]() .
.
∴|OB|=|t2|= ![]() .
.
∴|OA||OB|=2cosα ![]() =2tanα=2k.
=2tanα=2k.
∵k∈(1, ![]() ],∴2k∈(2,2
],∴2k∈(2,2 ![]() ].
].
∴|OA||OB|的取值范圍是(2,2 ![]() ]
]
【解析】(1)先將C1的參數方程化為普通方程,再華為極坐標方程,將C2的極坐標方程兩邊同乘ρ,根據極坐標與直角坐標的對應關系得出C2的直角坐標方程;(2)求出l的參數方程,分別代入C1 , C2的普通方程,根據參數的幾何意義得出|OA|,|OB|,得到|OA||OB|關于k的函數,根據k的范圍得出答案.


科目:高中數學 來源: 題型:
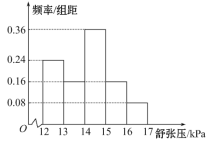
【題目】為研究某藥品的療效,選取若干名志愿者進行臨床試驗,所有志愿者的舒張壓數據(單位:![]() )的分組區間為
)的分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,將其按從左到右的順序分別編號為第一組,第二組,......,第五組.如圖是根據試驗數據制成的頻率分布直方圖.已知第一組與第二組共有
,將其按從左到右的順序分別編號為第一組,第二組,......,第五組.如圖是根據試驗數據制成的頻率分布直方圖.已知第一組與第二組共有![]() 人,第三組中沒有療效的有
人,第三組中沒有療效的有![]() 人,則第三組中有療效的人數為( )
人,則第三組中有療效的人數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
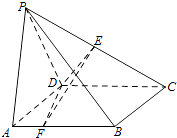
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,點E為線段PC的中點,點F在線段AB上. (Ⅰ)若AF=
,∠PDC=120°,點E為線段PC的中點,點F在線段AB上. (Ⅰ)若AF= ![]() ,求證:CD⊥EF;
,求證:CD⊥EF;
(Ⅱ)設平面DEF與平面DPA所成二面角的平面角為θ,試確定點F的位置,使得cosθ= ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)=ex﹣1﹣ax的圖象與x軸相切. (Ⅰ)求f(x)的單調區間;
(Ⅱ)當x>1時,f(x)>m(x﹣1)lnx,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學為調查來自南方和北方的同齡大學生的身高差異,從2016級的年齡在18~19歲之間的大學生中隨機抽取了來自南方和北方的大學生各10名,測量他們的身高,量出的身高如下(單位:cm):
南方:158,170,166,169,180,175,171,176,162,163.
北方:183,173,169,163,179,171,157,175,184,166.
(1)根據抽測結果,畫出莖葉圖,對來自南方和北方的大學生的身高作比較,寫出統計結論.
(2)設抽測的10名南方大學生的平均身高為![]() cm,將10名南方大學生的身高依次輸入如圖所示的程序框圖進行運算,問輸出的s大小為多少?并說明s的統計學意義。
cm,將10名南方大學生的身高依次輸入如圖所示的程序框圖進行運算,問輸出的s大小為多少?并說明s的統計學意義。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】觀察下列等式:12=1,12﹣22=﹣3,12﹣22+32=6,12﹣22+32﹣42=﹣10,…由以上等式推測到一個一般的結論:對于n∈N* , 12﹣22+32﹣42+…+(﹣1)n+1n2= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張三同學從每年生日時對自己的身高測量后記錄如表:
![]()
(附:回歸直線的斜率和截距的最小二乘法估計公式分別為: ,
,![]() )
)
(1)求身高![]() 關于年齡
關于年齡![]() 的線性回歸方程;(可能會用到的數據:
的線性回歸方程;(可能會用到的數據:![]() (cm))
(cm))
(2)利用(1)中的線性回歸方程,分析張三同學![]() 歲起到
歲起到![]() 歲身高的變化情況,如
歲身高的變化情況,如 ![]() 歲之前都符合這一變化,請預測張三同學
歲之前都符合這一變化,請預測張三同學 ![]() 歲時的身高。
歲時的身高。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com