
【題目】2020年初,由于疫情影響,開學延遲,為了不影響學生的學習,國務院、省市區教育行政部門倡導各校開展“停學不停課、停學不停教”,某校語文學科安排學生學習內容包含老師推送文本資料學習和視頻資料學習兩類,且這兩類學習互不影響已知其積分規則如下:每閱讀一篇文本資料積1分,每日上限積5分;觀看視頻1個積2分,每日上限積6分.經過抽樣統計發現,文本資料學習積分的概率分布表如表1所示,視頻資料學習積分的概率分布表如表2所示.
表1
文本學習積分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
視頻學習積分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)現隨機抽取1人了解學習情況,求其每日學習積分不低于9分的概率;
(2)現隨機抽取3人了解學習情況,設積分不低于9分的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
【答案】(1)![]() ;(2)分布列詳見解析,數學期望為
;(2)分布列詳見解析,數學期望為![]() .
.
【解析】
(1)由題意可得獲得的積分不低于(9分)的情形,因為兩類學習互不影響,根據相互獨立與互斥事件的概率計算公式即可得出概率![]() .
.
(2)隨機變量![]() 的所有可能取值為0,1,2,3.由(1)每個人積分不低于(9分)的概率為
的所有可能取值為0,1,2,3.由(1)每個人積分不低于(9分)的概率為![]() .根據二項分布列的概率計算公式即可得出.
.根據二項分布列的概率計算公式即可得出.
(1)由題意,獲得的積分不低于9分的情形共有(如下表所示):
文本 | 3 | 4 | 5 | 5 |
視頻 | 6 | 6 | 6 | 4 |
因為兩類學習情況互不影響,
所以每日學習積分不低于9分的概率![]() ,
,
即每日學習積分不低于9分的概率為![]() .
.
(2)隨機變量![]() 的所有可能取值為0,1,2,3
的所有可能取值為0,1,2,3
由(1)每個人積分不低于9分的概率為![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以隨機變量![]() 的概率分布列為:
的概率分布列為:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
可得![]() .
.
所以隨機變量![]() 的數學期望為
的數學期望為![]() .
.


科目:高中數學 來源: 題型:
【題目】某廠家準備在“6.18”舉行促銷活動,現根據近七年的廣告費與銷售量的數據確定此次廣告費支出.廣告費支出x(萬元)和銷售量y(萬臺)的數據如下:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
廣告費支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售量y | 1.8 | 3.0 | 4.0 | 4.2 | 5.0 | 5.3 | 5.4 |
(1)若用線性回歸模型擬合y與x的關系,求出y關于x的線性回歸方程(保留小數點后兩位);
(2)若用![]() 模型擬合y與x的關系,可得回歸方程
模型擬合y與x的關系,可得回歸方程![]() ,經計算線性回歸模型和該模型的R2分別約為0.774和0.888,請用R2說明選擇哪個回歸模型更好;
,經計算線性回歸模型和該模型的R2分別約為0.774和0.888,請用R2說明選擇哪個回歸模型更好;
(3)已知利潤z與x,y的關系為z=200y-x.根據(2)的結果,當廣告費x=20時,求銷售量及利潤的預報值.
參考公式:回歸直線![]() =
=![]() +
+![]() x的斜率和截距的最小二乘估計分別為
x的斜率和截距的最小二乘估計分別為![]() =
=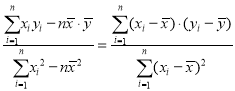 ,
,![]() .
.
參考數據:![]() ≈2.24,
≈2.24,![]() ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前,新冠病毒引發的肺炎疫情在全球肆虐,為了解新冠肺炎傳播途徑,采取有效防控措施,某醫院組織專家統計了該地區![]() 名患者新冠病毒潛伏期的相關信息,數據經過匯總整理得到如下圖所示的頻率分布直方圖(用頻率作為概率).潛伏期不高于平均數的患者,稱為“短潛伏者”,潛伏期高于平均數的患者,稱為“長潛伏者”.
名患者新冠病毒潛伏期的相關信息,數據經過匯總整理得到如下圖所示的頻率分布直方圖(用頻率作為概率).潛伏期不高于平均數的患者,稱為“短潛伏者”,潛伏期高于平均數的患者,稱為“長潛伏者”.
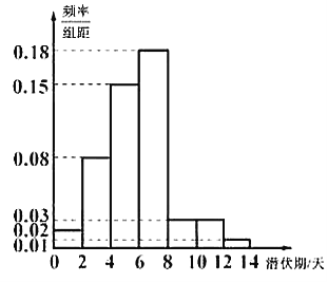
(1)求這![]() 名患者潛伏期的平均數(同一組中的數據用該組區間的中點值作代表),并計算出這
名患者潛伏期的平均數(同一組中的數據用該組區間的中點值作代表),并計算出這![]() 名患者中“長潛伏者”的人數;
名患者中“長潛伏者”的人數;
(2)現有![]() 名患者自愿報名某臨床試驗,其中“短潛伏者”
名患者自愿報名某臨床試驗,其中“短潛伏者”![]() 人,“長潛伏者”
人,“長潛伏者”![]() 人,醫生從
人,醫生從![]() 人中隨機抽取兩人做臨床試驗,求兩人中恰有
人中隨機抽取兩人做臨床試驗,求兩人中恰有![]() 人為“長潛伏者”的概率.
人為“長潛伏者”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在對人們休閑方式的一次調查中,共調查120人,其中女性70人,男性50人.女性中有40人主要的休閑方式是看電視,另外30人主要的休閑方式是運動;男性中有20人主要的休閑方式是看電視,另外30人主要的休閑方式是運動.
(1)請畫出性別與休閑方式的![]() 列聯表;
列聯表;
(2)能否在犯錯誤的概率不超過0.10的前提下,認為休閑方式與性別有關?
附: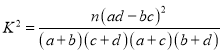 ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《山東省高考改革試點方案》規定:從2017年秋季高中入學的新生開始,不分文理科;2020年高考總成績由語數外三門統考科目和物理、化學等六門選考科目組成,將每門選考科目的考生原始成績從高到低劃分為![]() 、
、![]() 、
、![]() 、
、![]() 共8個等級,參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%,選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到
共8個等級,參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%,選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 八個分數區間,得到考生的等級成績.某市高一學生共6000人,為給高一學生合理選科提供依據,對六門選考科目進行測試,其中化學考試原始成績
八個分數區間,得到考生的等級成績.某市高一學生共6000人,為給高一學生合理選科提供依據,對六門選考科目進行測試,其中化學考試原始成績![]() 大致服從正態分布
大致服從正態分布![]() .
.
(1)求該市化學原始成績在區間![]() 的人數;
的人數;
(2)以各等級人數所占比例作為各分數區間發生的概率,按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區間![]() 的人數,求
的人數,求![]() .
.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數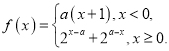 給出下列四個結論:①對
給出下列四個結論:①對![]() ,
,![]() ,使得
,使得![]() 無解;②對
無解;②對![]() ,
,![]() ,使得
,使得![]() 有兩解;③當
有兩解;③當![]() 時,
時,![]() ,使得
,使得![]() 有解;④當
有解;④當![]() 時,
時,![]() ,使得
,使得![]() 有三解.其中,所有正確結論的序號是______.
有三解.其中,所有正確結論的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() .已知點
.已知點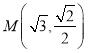 在橢圓上,且點M到兩焦點距離之和為4.
在橢圓上,且點M到兩焦點距離之和為4.
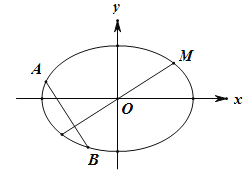
(1)求橢圓的方程;
(2)設與MO(O為坐標原點)垂直的直線交橢圓于A,B(A,B不重合),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關說法正確的是( )
A.![]() 的展開式中含
的展開式中含![]() 項的二項式系數為20;
項的二項式系數為20;
B.事件![]() 為必然事件,則事件
為必然事件,則事件![]() 、
、![]() 是互為對立事件;
是互為對立事件;
C.設隨機變量![]() 服從正態分布
服從正態分布![]() ,若
,若![]() ,則
,則![]() 與
與![]() 的值分別為
的值分別為![]() ,
,![]() ;
;
D.甲、乙、丙、丁4個人到4個景點旅游,每人只去一個景點,設事件![]() “4個人去的景點各不相同”,事件
“4個人去的景點各不相同”,事件![]() “甲獨自去一個景點”,則
“甲獨自去一個景點”,則![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com