
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,且過點A(2,1).
,且過點A(2,1).
(1)求C的方程:
(2)點M,N在C上,且AM⊥AN,AD⊥MN,D為垂足.證明:存在定點Q,使得|DQ|為定值.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
(1)由題意得到關于a,b,c的方程組,求解方程組即可確定橢圓方程.
(2)設出點M,N的坐標,在斜率存在時設方程為![]() , 聯立直線方程與橢圓方程,根據已知條件,已得到m,k的關系,進而得直線MN恒過定點,在直線斜率不存在時要單獨驗證,然后結合直角三角形的性質即可確定滿足題意的點Q的位置.
, 聯立直線方程與橢圓方程,根據已知條件,已得到m,k的關系,進而得直線MN恒過定點,在直線斜率不存在時要單獨驗證,然后結合直角三角形的性質即可確定滿足題意的點Q的位置.
(1)由題意可得: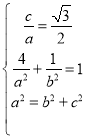 ,解得:
,解得:![]() ,故橢圓方程為:
,故橢圓方程為:![]() .
.
(2)設點![]() .
.
因為AM⊥AN,∴![]() ,即
,即![]() ,①
,①
當直線MN的斜率存在時,設方程為![]() ,如圖1.
,如圖1.
代入橢圓方程消去![]() 并整理得:
并整理得:![]() ,
,
![]() ②,
②,
根據![]() ,代入①整理可得:
,代入①整理可得:
![]()
將②代入,![]() ,
,
整理化簡得![]() ,
,
∵![]() 不在直線
不在直線![]() 上,∴
上,∴![]() ,
,
∴![]() ,
,
于是MN的方程為![]() ,
,
所以直線過定點直線過定點![]() .
.
當直線MN的斜率不存在時,可得![]() ,如圖2.
,如圖2.
代入![]() 得
得![]() ,
,
結合![]() ,解得
,解得![]() ,
,
此時直線MN過點![]() ,
,
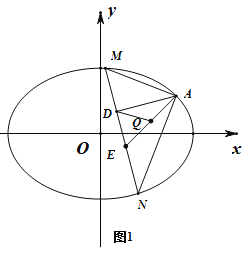
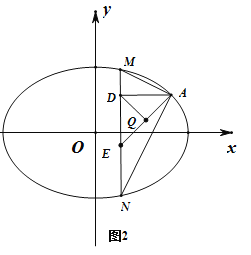
由于AE為定值,且△ADE為直角三角形,AE為斜邊,
所以AE中點Q滿足![]() 為定值(AE長度的一半
為定值(AE長度的一半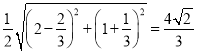 ).
).
由于![]() ,故由中點坐標公式可得
,故由中點坐標公式可得![]() .
.
故存在點![]() ,使得|DQ|為定值.
,使得|DQ|為定值.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:
【題目】將某公司200天的日銷售收入(單位:萬元)統計如下表(1)所示,
日銷售收入 |
|
|
|
|
|
|
頻數 | 12 | 28 | 36 | 54 | 50 | 20 |
頻率 |
表(1)
(1)完成上述頻率分布表,并估計公司這200天的日均銷售收入(同一組中的數據用該組所在區間的中點值代表);
(2)已知該公司2020年第一、二季度的日銷售收入如下表(2)所示,第三季度的日銷售收入及其頻率可用表(1)中的數據近似代替,且在2020年,當公司日銷售收入為![]() 時,員工的日績效為100元,當公司日銷售收入為
時,員工的日績效為100元,當公司日銷售收入為![]() 時,員工的日績效為200元,當公司日銷售收入為
時,員工的日績效為200元,當公司日銷售收入為![]() 時,員工的日績效為300元.以頻率估計概率.
時,員工的日績效為300元.以頻率估計概率.
①若在第三季度某員工的工作日中隨機抽取2天,記該員工2天的績效之和為![]() ,求
,求![]() 的分布列以及數學期望;
的分布列以及數學期望;
②若每個員工每個季度的工作日為50天,估計2020年前三個季度每個員工獲得的績效的總額.
日銷售收入 |
|
|
|
|
|
|
頻率 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 |
表(2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為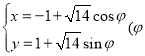 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .曲線
.曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 與曲線
與曲線![]() 的交線為直線
的交線為直線![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與曲線
,與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為原點,拋物線![]() 的準線與y軸的交點為H,P為拋物線C上橫坐標為4的點,已知點P到準線的距離為5.
的準線與y軸的交點為H,P為拋物線C上橫坐標為4的點,已知點P到準線的距離為5.
(1)求C的方程;
(2)過C的焦點F作直線l與拋物線C交于A,B兩點,若以AH為直徑的圓過B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
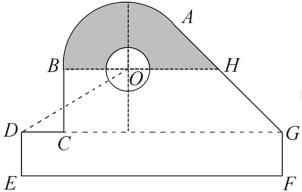
【題目】某中學開展勞動實習,學生加工制作零件,零件的截面如圖所示.O為圓孔及輪廓圓弧AB所在圓的圓心,A是圓弧AB與直線AG的切點,B是圓弧AB與直線BC的切點,四邊形DEFG為矩形,BC⊥DG,垂足為C,tan∠ODC=![]() ,
,![]() ,EF=12 cm,DE=2 cm,A到直線DE和EF的距離均為7 cm,圓孔半徑為1 cm,則圖中陰影部分的面積為________cm2.
,EF=12 cm,DE=2 cm,A到直線DE和EF的距離均為7 cm,圓孔半徑為1 cm,則圖中陰影部分的面積為________cm2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為直角梯形,AB//CD,
中,底面ABCD為直角梯形,AB//CD,![]()
![]() 是以
是以![]() 為斜邊的等腰直角三角形,且平面
為斜邊的等腰直角三角形,且平面![]() 平面ABCD,點F滿足,
平面ABCD,點F滿足,![]() .
.
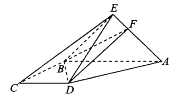
(1)試探究![]() 為何值時,CE//平面BDF,并給予證明;
為何值時,CE//平面BDF,并給予證明;
(2)在(1)的條件下,求直線AB與平面BDF所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左焦點
的左焦點![]() ,點
,點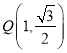 在橢圓
在橢圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)經過圓![]() :
:![]() 上一動點
上一動點![]() 作橢圓
作橢圓![]() 的兩條切線,切點分別記為
的兩條切線,切點分別記為![]() ,
,![]() ,直線
,直線![]() ,
,![]() 分別與圓
分別與圓![]() 相交于異于點
相交于異于點![]() 的
的![]() ,
,![]() 兩點.
兩點.
(i)當直線![]() ,
,![]() 的斜率都存在時,記直線
的斜率都存在時,記直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .求證:
.求證:![]() ;
;
(ii)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在新中國成立70周年國慶閱兵慶典中,眾多群眾在臉上貼著一顆紅心,以此表達對祖國的熱愛之情,在數學中,有多種方程都可以表示心型曲線,其中有著名的笛卡爾心型曲線,如圖,在直角坐標系中,以原點O為極點,x軸正半軸為極軸建立極坐標系.圖中的曲線就是笛卡爾心型曲線,其極坐標方程為![]() (
(![]() ),M為該曲線上的任意一點.
),M為該曲線上的任意一點.
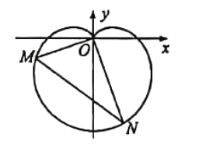
(1)當![]() 時,求M點的極坐標;
時,求M點的極坐標;
(2)將射線OM繞原點O逆時針旋轉![]() 與該曲線相交于點N,求
與該曲線相交于點N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
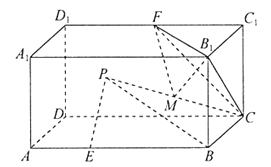
【題目】古希臘數學家阿波羅尼奧斯發現:平面上到兩定點![]() ,
,![]() 距離之比為常數
距離之比為常數![]() 且
且![]() 的點的軌跡是一個圓心在直線
的點的軌跡是一個圓心在直線![]() 上的圓,該圓簡稱為阿氏圓.根據以上信息,解決下面的問題:如圖,在長方體
上的圓,該圓簡稱為阿氏圓.根據以上信息,解決下面的問題:如圖,在長方體![]() 中,
中,![]() ,點
,點![]() 在棱
在棱![]() 上,
上,![]() ,動點
,動點![]() 滿足
滿足![]() .若點
.若點![]() 在平面
在平面![]() 內運動,則點
內運動,則點![]() 所形成的阿氏圓的半徑為________;若點
所形成的阿氏圓的半徑為________;若點![]() 在長方體
在長方體![]() 內部運動,
內部運動,![]() 為棱
為棱![]() 的中點,
的中點,![]() 為
為![]() 的中點,則三棱錐
的中點,則三棱錐![]() 的體積的最小值為___________.
的體積的最小值為___________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com