
已知函數(shù) 函數(shù)
函數(shù) 是區(qū)間
是區(qū)間 上的減函數(shù). ①當
上的減函數(shù). ①當 曲線
曲線 在點
在點 的切線
的切線 與
與 軸、
軸、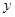 軸圍成的三角形面積為
軸圍成的三角形面積為 ,求
,求 的最大值;
的最大值;
②若 時恒成立,求t的取值范圍;
時恒成立,求t的取值范圍;
③ 試判定函數(shù)
試判定函數(shù) 在區(qū)間
在區(qū)間 內的零點個數(shù),并作出證明.
內的零點個數(shù),并作出證明.
①因為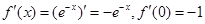 ,切線
,切線 的斜率為
的斜率為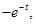 切點
切點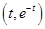
故切線 的方程為
的方程為 即
即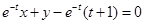 ,…1分
,…1分
令 得
得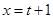 ,又令
,又令 得
得
所以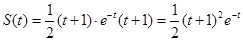 ……………2分
……………2分
從而
∵當 時,
時, ,當
,當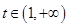 時,
時, ,
,
所以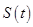 的最大值為
的最大值為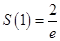 ……………4分
……………4分
②由①知: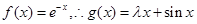 ,
,
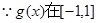 上單調遞減,
上單調遞減,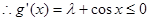
即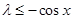 在[-1,1]上恒成立,
在[-1,1]上恒成立,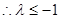 ……………6分
……………6分
要使 時恒成立
時恒成立
因
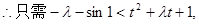
 (其中
(其中 )恒成立,
)恒成立,
令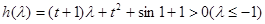 ,
,
則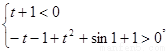
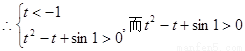 恒成立,
恒成立,
 ……………9分
……………9分
③函數(shù) 連續(xù),且
連續(xù),且

當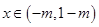 時,
時, 為減函數(shù),
為減函數(shù),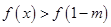
當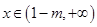 時,
時, 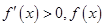 為增函數(shù),
為增函數(shù), 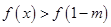
根據(jù)函數(shù)極值判別方法,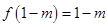 為極小值,而且
為極小值,而且
對 都有
都有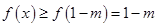
故當整數(shù)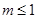 時,
時,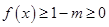 ……………11分
……………11分
所以當整數(shù)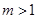 時,
時,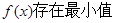
 ,
,
函數(shù)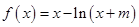 在
在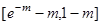 上為連續(xù)減函數(shù).
上為連續(xù)減函數(shù).
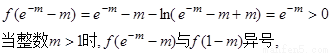
由所給定理知,存在唯一的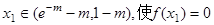
而當整數(shù)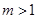 時,
時,
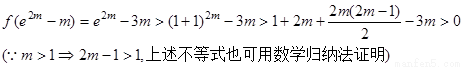 ………13分
………13分
類似地,當整數(shù)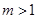 時,函數(shù)
時,函數(shù)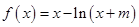 在
在 上為連續(xù)增函數(shù)且
上為連續(xù)增函數(shù)且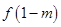 與
與 異號,由所給定理知,存在唯一的
異號,由所給定理知,存在唯一的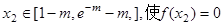 故當
故當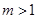 時,方程
時,方程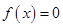 在
在 內有兩個實根
………15分
內有兩個實根
………15分
【解析】略


科目:高中數(shù)學 來源:東北師大附中2006—2007學年度上學期高三年級第二次質量檢測、數(shù)學(理)試題 題型:013
已知函數(shù)![]() 處取到極大值,則下面的結論正確的是
處取到極大值,則下面的結論正確的是
A.函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù).
上是減函數(shù).
B.函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù).
上是減函數(shù).
C.函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù).
上是增函數(shù).
D.函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù).
上是增函數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年江西省高三第四次月考理科數(shù)學試卷 題型:解答題
已知函數(shù):
(1)討論函數(shù) 的單調性;
的單調性;
(2)若函數(shù) 的圖象在點
的圖象在點 處的切線的傾斜角為45o,對于任意的
處的切線的傾斜角為45o,對于任意的 ,函數(shù)
,函數(shù) 在區(qū)間
在區(qū)間 上總不是單調函數(shù),求m的取值范圍;
上總不是單調函數(shù),求m的取值范圍;
(3)求證:. (
(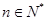 且
且 )
)
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年河南省焦作市高三第一學期期末考試數(shù)學文卷 題型:選擇題
已知函數(shù)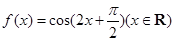 ,下面結論錯誤的是
,下面結論錯誤的是
A.函數(shù)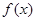 的最小正周期為
的最小正周期為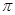 B.函數(shù)
B.函數(shù)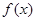 是奇函數(shù)
是奇函數(shù)
C.函數(shù)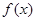 的圖象關于直線
的圖象關于直線 對稱
D.函數(shù)
對稱
D.函數(shù)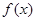 在區(qū)間
在區(qū)間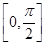 上是減函數(shù)
上是減函數(shù)
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年河南省焦作市高三期末調研數(shù)學理卷 題型:選擇題
已知函數(shù)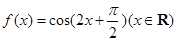 ,下面結論錯誤的是
,下面結論錯誤的是
A.函數(shù)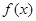 的最小正周期為
的最小正周期為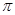 B.函數(shù)
B.函數(shù)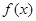 是奇函數(shù)
是奇函數(shù)
C.函數(shù)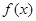 的圖象關于直線
的圖象關于直線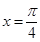 對稱
D.函數(shù)
對稱
D.函數(shù)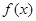 在區(qū)間
在區(qū)間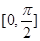 上是減函數(shù)
上是減函數(shù)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com