
【題目】設a,b是不同的直線,α,β是不同的平面,則下列四個命題中正確的是________.(填序號)
① 若a⊥b,a⊥α,則b∥α;② 若a∥α,α⊥β,則a⊥β;
③ 若a⊥β,α⊥β,則a∥α;④ 若a⊥b,a⊥α,b⊥β,則α⊥β.
【答案】④
【解析】對于①,根據![]() ,則
,則![]() 或
或![]() ,不一定得出
,不一定得出![]() ,由此可得①不正確;對于②,若a∥α,α⊥β,則可能
,由此可得①不正確;對于②,若a∥α,α⊥β,則可能![]() ,因此②不正確;;對于③,
,因此②不正確;;對于③,![]() ,則
,則![]() 或
或![]() ,不一定得出
,不一定得出![]() ,由此可得③不正確;對于④,由
,由此可得③不正確;對于④,由![]() 且
且![]() ,可得直線
,可得直線![]() 所成角或其補角等于平面
所成角或其補角等于平面![]() 所成角,又因為
所成角,又因為![]() ,可得直線
,可得直線![]() 所成角對于
所成角對于![]() ,由此可得
,由此可得![]() ,所以④是真命題,綜上所述,可得正確命題的序號為④,故答案為④.
,所以④是真命題,綜上所述,可得正確命題的序號為④,故答案為④.
【方法點晴】本題主要考查線面平行的判定與性質、面面垂直的性質及線面垂直的判定,屬于難題.空間直線、平面平行或垂直等位置關系命題的真假判斷,常采用畫圖(尤其是畫長方體)、現實實物判斷法(如墻角、桌面等)、排除篩選法等;另外,若原命題不太容易判斷真假,可以考慮它的逆否命題,判斷它的逆否命題真假,原命題與逆否命題等價.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,以坐標原點為極點,![]() 軸為正半軸建立極坐標系,圓
軸為正半軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為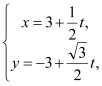 (t為參數).
(t為參數).
(1)求圓![]() 的直角坐標方程;
的直角坐標方程;
(2)求直線![]() 分圓
分圓![]() 所得的兩弧程度之比.
所得的兩弧程度之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
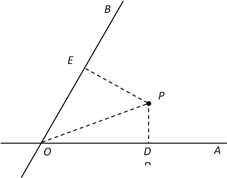
【題目】如圖,![]() 、
、![]() 是兩條公路(近似看成兩條直線),
是兩條公路(近似看成兩條直線),![]() ,在
,在![]() 內有一紀念塔
內有一紀念塔![]() (大小忽略不計),已知
(大小忽略不計),已知![]() 到直線
到直線![]() 、
、![]() 的距離分別為
的距離分別為![]() 、
、![]() ,
,![]() =6千米,
=6千米,![]() =12千米.現經過紀念塔
=12千米.現經過紀念塔![]() 修建一條直線型小路,與兩條公路
修建一條直線型小路,與兩條公路![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() .
.
(1)求紀念塔![]() 到兩條公路交點
到兩條公路交點![]() 處的距離;
處的距離;
(2)若紀念塔![]() 為小路
為小路![]() 的中點,求小路
的中點,求小路![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() (
(![]() ).
).
(1)證明:直線![]() 過定點;
過定點;
(2)若直線不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 軸負半軸于
軸負半軸于![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,△
,△![]() 的面積為
的面積為![]() (
(![]() 為坐標原點),求
為坐標原點),求![]() 的最小值,并求此時直線
的最小值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABCA1B1C1中, CC1⊥平面ABC, AC⊥BC, AB1的中點為D,B1C∩BC1=E. 求證:
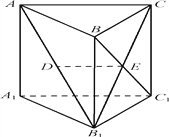
(1)DE∥平面AA1C1C;
(2)AC⊥平面BCC1B1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:![]() .
.
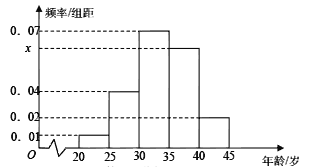
(Ⅰ)求圖中![]() 的值,并根據頻率分布直方圖估計這500名志愿者中年齡在
的值,并根據頻率分布直方圖估計這500名志愿者中年齡在![]() 歲的人數;
歲的人數;
(Ⅱ)在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取10名參加中心廣場的宣傳活動,再從這10名志愿者中選取3名擔任主要負責人.記這3名志愿者中“年齡低于35歲”的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知國家某5A級大型景區對擁擠等級與每日游客數量![]() (單位:百人)的關系有如下規定:當
(單位:百人)的關系有如下規定:當![]()
![]() 時,擁擠等級為“優”;當
時,擁擠等級為“優”;當![]()
![]() 時,擁擠等級為“良”;當
時,擁擠等級為“良”;當![]()
![]() 時,擁擠等級為“擁擠”;當
時,擁擠等級為“擁擠”;當![]()
![]() 時,擁擠等級為“嚴重擁擠”。該景區對6月份的游客數量作出如圖的統計數據:
時,擁擠等級為“嚴重擁擠”。該景區對6月份的游客數量作出如圖的統計數據:
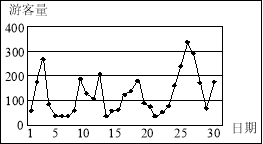
(Ⅰ)下面是根據統計數據得到的頻率分布表,求出![]() 的值,并估計該景區6月份游客人數的平均值(同一組中的數據用該組區間的中點值作代表);
的值,并估計該景區6月份游客人數的平均值(同一組中的數據用該組區間的中點值作代表);
游客數量 (單位:百人) |
|
|
|
|
天數 |
|
|
|
|
頻率 |
|
|
|
|
(Ⅱ)某人選擇在6月1日至6月5日這5天中任選2天到該景區游玩,求他這2天遇到的游客擁擠等級均為“優”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com