
【題目】已知a、b、c為![]() 的三邊長,直線
的三邊長,直線![]() 的方程為
的方程為![]() ,圓
,圓![]() .
.
(1)若![]() 為直角三角形,c為斜邊長,且直線
為直角三角形,c為斜邊長,且直線![]() 與圓M相切.求c的值;
與圓M相切.求c的值;
(2)已知![]() 為坐標原點,點
為坐標原點,點![]() ,
,![]() ,
,![]() ,
,![]() ,平行于ON的直線h與圓M相交于R,
,平行于ON的直線h與圓M相交于R,![]() 兩點,且
兩點,且![]() ,求直線h的方程:
,求直線h的方程:
(3)若![]() 為正三角形,對于直線
為正三角形,對于直線![]() 上任意一點P,在圓
上任意一點P,在圓![]() 上總存在一點
上總存在一點![]() ,使得線段
,使得線段![]() 的長度為整數,求c的取值范圍;
的長度為整數,求c的取值范圍;
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]() .
.
【解析】
(1)![]() 為直角三角形,
為直角三角形,![]() 為斜邊長,則
為斜邊長,則![]() ,又直線與圓相切,根據點到直線的距離公式,得到關于
,又直線與圓相切,根據點到直線的距離公式,得到關于![]() 的方程,求出
的方程,求出![]() 即可.
即可.
(2)由直線![]() 平行于
平行于![]() 計算出斜率,設直線h的方程為
計算出斜率,設直線h的方程為![]() ,利用點到線的距離公式求距離,勾股定理得到方程,即可求出參數
,利用點到線的距離公式求距離,勾股定理得到方程,即可求出參數![]() 。
。
(3)此時圓為以![]() 為圓心,以
為圓心,以![]() 為半徑的圓,直線可化為
為半徑的圓,直線可化為![]() ,直線
,直線![]() 上任意一點
上任意一點![]() ,在圓
,在圓![]() 上總存在一點
上總存在一點![]() ,使得線段
,使得線段![]() 的長度為整數,設圓心到直線的距離為
的長度為整數,設圓心到直線的距離為![]() ,只需
,只需![]() 能用整數表示,并且圓的直徑
能用整數表示,并且圓的直徑![]() 即可.
即可.
解:(1)由題意得![]() ,
,
圓心到直線的距離,
![]() 或0(舍)
或0(舍)
綜上:![]() .
.
(2)圓M的標準方程為![]() ,
,
所以圓心![]() ,半徑為5.
,半徑為5.
因為直線![]() ,所以直線h的斜率為
,所以直線h的斜率為![]() .
.
設直線h的方程為![]() ,即
,即![]() ,
,
則圓心M到直線h的距離![]() .
.
因為![]()
而![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() .
.
故直線h的方程為![]() 或
或![]() .
.
(3)![]() 為正三角形,
為正三角形,
![]() ,直線
,直線![]() ,
,
![]() ,對于這條直線,總存在無窮多點在圓外,
,對于這條直線,總存在無窮多點在圓外,
從中找一個到圓心距離為![]() 的點P,則點P到圖上任意點
的點P,則點P到圖上任意點![]() 的距離,
的距離,
![]() ,
,![]() 時不存在整數,
時不存在整數,
![]() ;下面分類討論:
;下面分類討論:
(Ⅰ)直線與圓相切或相離,即![]() ;即
;即![]() ;
;
此時![]() ,所以
,所以![]() 可以取到整數.
可以取到整數.
(Ⅱ)線與圓相交,即![]() ,直線上不在圓內的點P,同理成立;
,直線上不在圓內的點P,同理成立;
對于直線上在圓內部分的任意點P,![]() ,
,
![]() ,
,
![]()
所以使得![]() 存在整數的條件是
存在整數的條件是![]() 對任意點P都成立,
對任意點P都成立,
![]() ,
,![]() ,
,![]()
所以![]() ,
,
綜上![]() .
.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且左焦點F1到左準線的距離為4.
,且左焦點F1到左準線的距離為4.

(1)求橢圓![]() 的方程;
的方程;
(2)若與原點距離為1的直線l1:![]() 與橢圓
與橢圓![]() 相交于A,B兩點,直線l2與l1平行,且與橢圓
相交于A,B兩點,直線l2與l1平行,且與橢圓![]() 相切于點M(O,M位于直線l1的兩側).記△MAB,△OAB的面積分別為S1,S2,若
相切于點M(O,M位于直線l1的兩側).記△MAB,△OAB的面積分別為S1,S2,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() ,
,![]() .
.
(1)以過原點的直線的傾斜角![]() 為參數,寫出曲線
為參數,寫出曲線![]() 的參數方程;
的參數方程;
(2)直線![]() 過原點,且與曲線
過原點,且與曲線![]() ,
,![]() 分別交于
分別交于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 不是原點)。求
不是原點)。求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著小汽車的普及,“駕駛證”已經成為現代人“必考”的證件之一.若某人報名參加了駕駛證考試,要順利地拿到駕駛證,他需要通過四個科目的考試,其中科目二為場地考試.在一次報名中,每個學員有5次參加科目二考試的機會(這5次考試機會中任何一次通過考試,就算順利通過,即進入下一科目考試;若5次都沒有通過,則需重新報名),其中前2次參加科目二考試免費,若前2次都沒有通過,則以后每次參加科目二考試都需要交200元的補考費.某駕校對以往2000個學員第1次參加科目二考試進行了統計,得到下表:
考試情況 | 男學員 | 女學員 |
第1次考科目二人數 | 1200 | 800 |
第1次通過科目二人數 | 960 | 600 |
第1次未通過科目二人數 | 240 | 200 |
若以上表得到的男、女學員第1次通過科目二考試的頻率分別作為此駕校男、女學員每次通過科目二考試的概率,且每人每次是否通過科目二考試相互獨立.現有一對夫妻同時在此駕校報名參加了駕駛證考試,在本次報名中,若這對夫妻參加科目二考試的原則為:通過科目二考試或者用完所有機會為止.
(1)求這對夫妻在本次報名中參加科目二考試都不需要交補考費的概率;
(2)若這對夫妻前2次參加科目二考試均沒有通過,記這對夫妻在本次報名中參加科目二考試產生的補考費用之和為![]() 元,求
元,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某校學生每周課外閱讀的情況,采用分層抽樣的方法,收集100位學生每周課外閱讀時間的樣本數據(單位:小時).根據這100個數據,制作出學生每周課外閱讀時間的頻率分布直方圖(如圖).
(1)估計這100名學生每周課外閱讀的平均數![]() 和樣本方差
和樣本方差![]() (同一組數據用該組區間的中點值作代表);
(同一組數據用該組區間的中點值作代表);
(2)由頻率分布直方圖知,該校學生每周課外閱讀時間![]() 近似服從正態分布
近似服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
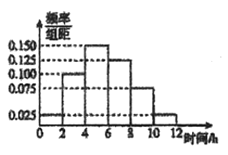
①求![]() ;
;
②若該校共有10000名學生,記每周課外閱讀時間在區間![]() 的人數為
的人數為![]() ,試求
,試求![]() .
.
參數數據:![]() ,若
,若![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱 ABC﹣A1B1C1 中,AB 1 ,若二面角 C AB C1 的大小為 60°,則點 C 到平面 ABC1 的距離為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱 ABC A1 B1C1 中, AB 3 , AA1 4 , M 為 AA1 的中點, P 是 BC 上一點,且由 P 沿棱柱側面經過棱 CC1 到 M 點的最短路線長為![]() ,設這條最短路線與 CC1 的交點為 N 。求:
,設這條最短路線與 CC1 的交點為 N 。求:
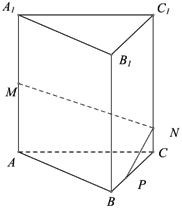
(1)該三棱柱的側面展開圖的對角線長;
(2) PC 和 NC 的長;
(3)平面 NMP 和平面 ABC 所成銳二面角大小的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 在其圖象上存在不同的兩點
在其圖象上存在不同的兩點![]() ,
,![]() ,其坐標滿足條件:
,其坐標滿足條件:![]() 的最大值為0,則稱
的最大值為0,則稱![]() 為“柯西函數”,
為“柯西函數”,
則下列函數:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
其中為“柯西函數”的個數為![]()
![]()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓C:![]() 過點M(2,0),且右焦點為F(1,0),過F的直線l與橢圓C相交于A、B兩點.設點P(4,3),記PA、PB的斜率分別為k1和k2.
過點M(2,0),且右焦點為F(1,0),過F的直線l與橢圓C相交于A、B兩點.設點P(4,3),記PA、PB的斜率分別為k1和k2.

(1)求橢圓C的方程;
(2)如果直線l的斜率等于-1,求出k1k2的值;
(3)探討k1+k2是否為定值?如果是,求出該定值;如果不是,求出k1+k2的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com