
【題目】已知函數(shù)![]() ,
, ![]() ,
, ![]() ,且
,且![]() 的最小值為
的最小值為![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 對任意
對任意![]() 恒成立,其中
恒成立,其中![]() 是自然對數(shù)的底數(shù),求
是自然對數(shù)的底數(shù),求![]() 的取值范圍;
的取值范圍;
(3)設(shè)曲線![]() 與曲線
與曲線![]() 交于點
交于點![]() ,且兩曲線在點
,且兩曲線在點![]() 處的切線分別為
處的切線分別為![]() ,
, ![]() .試判斷
.試判斷![]() ,
, ![]() 與
與![]() 軸是否能圍成等腰三角形?若能,確定所圍成的等腰三角形的個數(shù);若不能,請說明理由.
軸是否能圍成等腰三角形?若能,確定所圍成的等腰三角形的個數(shù);若不能,請說明理由.
【答案】(1)![]() .(2)
.(2)![]() . (3)
. (3)![]() ,
, ![]() 與
與![]() 軸能圍成2個等腰三角形.
軸能圍成2個等腰三角形.
【解析】試題分析:
(1)由原函數(shù)與導(dǎo)函數(shù)的關(guān)系可求得a=-2;
(2) 不等式即![]() ,構(gòu)造函數(shù)令
,構(gòu)造函數(shù)令![]() ,分類討論可得
,分類討論可得![]() 的取值范圍是
的取值范圍是![]() .
.
(3) 設(shè)![]() ,
, ![]() 的傾斜角分別為
的傾斜角分別為![]() ,
, ![]() ,若
,若![]() ,
, ![]() 與
與![]() 軸所圍成的三角形是等腰三角形,則
軸所圍成的三角形是等腰三角形,則![]() 或
或![]() . 分類討論:
. 分類討論: ![]() 和
和![]() 兩種情況可得
兩種情況可得![]() ,
, ![]() 與
與![]() 軸能圍成2個等腰三角形.
軸能圍成2個等腰三角形.
試題解析:
(1)![]() ,所以
,所以![]() ,則
,則![]() 的最小值為
的最小值為![]() ,
,
因此拋物線![]() 的對稱軸為
的對稱軸為![]() ,即
,即![]() ,所以
,所以![]() .
.
(2)由(1)知, ![]() .不等式
.不等式![]() 即
即![]() ,
,
所以![]() 對任意
對任意![]() 恒成立.
恒成立.
令![]() ,則
,則![]() .
.
①若![]() ,則
,則![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)減,
上單調(diào)減,
故![]() ,解得
,解得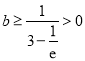 ,
,
此時無符合題意的![]() 值; ②若
值; ②若![]() ,令
,令![]() ,解得
,解得![]() .
.
列表如下:
|
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ |
由題意,可知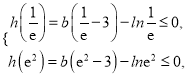 解得
解得![]() .
.
故![]() 的取值范圍為
的取值范圍為![]() .
.
(3)設(shè)![]() ,
, ![]() 的傾斜角分別為
的傾斜角分別為![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
因為![]() ,所以
,所以![]() ,
, ![]() ,則
,則![]() ,
, ![]() 均為銳角.
均為銳角.
若![]() ,
, ![]() 與
與![]() 軸所圍成的三角形是等腰三角形,則
軸所圍成的三角形是等腰三角形,則![]() 或
或![]() .
.
①當(dāng)![]() 時,
時, ![]() ,即
,即![]() ,解得
,解得![]() ,
,
而![]() ,即
,即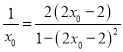 ,
,
整理得, ![]() ,解得
,解得![]() .
.
所以存在唯一的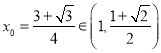 滿足題意.
滿足題意.
②當(dāng)![]() 時,由
時,由![]() 可得
可得![]() ,
,
而![]() ,即
,即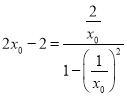 ,
,
整理得, ![]() .
.
令![]() ,則
,則![]() .
.
令![]() ,解得
,解得![]() .列表如下:
.列表如下:
|
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ |
而![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 在
在![]() 內(nèi)有一個零點,也是
內(nèi)有一個零點,也是![]() 上的唯一零點.
上的唯一零點.
所以存在唯一的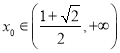 滿足題意.
滿足題意.
綜上所述, ![]() ,
, ![]() 與
與![]() 軸能圍成2個等腰三角形.
軸能圍成2個等腰三角形.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線x2=2py(p>0)與直線2x﹣y+1=0交于A,B兩點, ![]() ,點M在拋物線上,MA⊥MB.
,點M在拋物線上,MA⊥MB. 
(1)求p的值;
(2)求點M的橫坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)f(x)=x2+bx+c,且f(﹣3)=f(1),f(0)=0.
(1)求函數(shù)f(x)的解析式;
(2)若函數(shù)g(x)=f(x)﹣(4+2a)x+2,x∈[1,2],求函數(shù)g(x)的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《張邱建算經(jīng)》是中國古代數(shù)學(xué)史上的杰作,該書中有首古民謠記載了一數(shù)列問題:“南山一棵竹, 竹尾風(fēng)割斷, 剩下三十節(jié),一節(jié)一個圈. 頭節(jié)高五寸①,頭圈一尺三②.逐節(jié)多三分③,逐圈少分三④. 一蟻往上爬,遇圈則繞圈. 爬到竹子頂,行程是多遠?”(注釋:①第一節(jié)的高度為![]() 尺;②第一圈的周長為
尺;②第一圈的周長為![]() 尺;③每節(jié)比其下面的一節(jié)多
尺;③每節(jié)比其下面的一節(jié)多![]() 尺;④每圈周長比其下面的一圈少
尺;④每圈周長比其下面的一圈少![]() 尺) 問:此民謠提出的問題的答案是
尺) 問:此民謠提出的問題的答案是
A. ![]() 尺 B.
尺 B. ![]() 尺
尺
C. ![]() 尺 D.
尺 D. ![]() 尺
尺
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E: ![]() ,不經(jīng)過原點O的直線l:y=kx+m(k>0)與橢圓E相交于不同的兩點A、B,直線OA,AB,OB的斜率依次構(gòu)成等比數(shù)列.
,不經(jīng)過原點O的直線l:y=kx+m(k>0)與橢圓E相交于不同的兩點A、B,直線OA,AB,OB的斜率依次構(gòu)成等比數(shù)列. 
(Ⅰ)求a,b,k的關(guān)系式;
(Ⅱ)若離心率 ![]() 且
且 ![]() ,當(dāng)m為何值時,橢圓的焦距取得最小值?
,當(dāng)m為何值時,橢圓的焦距取得最小值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=x2﹣4x+3,若f(x)≥mx對任意的實數(shù)x≥2都成立,則實數(shù)m的取值范圍是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=loga(x2﹣2ax)(a>0且a≠1)滿足對任意的x1 , x2∈[3,4],且x1≠x2時,都有 ![]() >0成立,則實數(shù)a的取值范圍是
>0成立,則實數(shù)a的取值范圍是
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com