
【題目】在![]() 中,設邊
中,設邊![]() ,
,![]() ,
,![]() 所對的角分別為
所對的角分別為![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用正弦定理可將原式化簡為cosA![]() sinA
sinA![]() ,整理得
,整理得![]() sinC﹣cosC=1,即sin(C
sinC﹣cosC=1,即sin(C![]() )
)![]() ,進而可得C的大小;
,進而可得C的大小;
(2)利用余弦定理可將cosB![]() 化成
化成![]() ,即8sinAcosB=5sinC=5sin
,即8sinAcosB=5sinC=5sin![]() ,進而求出sinAcosB的值.
,進而求出sinAcosB的值.
(1)△ABC中,![]() ,即cosA
,即cosA![]() sinA
sinA![]() ,
,
∴sinCcosA![]() sinAsinC=sinB+sinA,
sinAsinC=sinB+sinA,
∵sinB+sinA=sin(A+C)+sinA=sinAcosC+sinCcosA+sinA,
∴sinCcosA![]() sinAsinC=sinAcosC+sinCcosA+sinA,可得
sinAsinC=sinAcosC+sinCcosA+sinA,可得![]() sinAsinC=sinAcosC+sinA,
sinAsinC=sinAcosC+sinA,
∵sinA≠0,
∴![]() sinC﹣cosC=1,即sin(C
sinC﹣cosC=1,即sin(C![]() )
)![]() ,
,
∵C∈(0,π),C![]() ∈(
∈(![]() ,
,![]() ),
),
∴C![]() ,可得C
,可得C![]() .
.
(2)若![]() ,則cosB
,則cosB![]() ,即8sinAcosB=5sinC=5sin
,即8sinAcosB=5sinC=5sin![]() ,
,
所以sinAcosB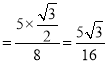 .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,動點
中,動點![]() (其中
(其中![]() )到點
)到點![]() 的距離的
的距離的![]() 倍與點
倍與點![]() 到直線
到直線![]() 的距離的
的距離的![]() 倍之和記為
倍之和記為![]() ,且
,且![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設過點![]() 的直線
的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)=a![]() (a為常數).
(a為常數).
(1)求a的值;
(2)若函數g(x)=|(2x+1)f(x)|﹣k有2個零點,求實數k的取值范圍;
(3)若x∈[﹣2,﹣1]時,不等式f(x)![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的方程為
的方程為![]() ,橢圓
,橢圓![]() 的離心率正好是雙曲線
的離心率正好是雙曲線![]() 的離心率的倒數,橢圓
的離心率的倒數,橢圓![]() 的短軸長等于拋物線
的短軸長等于拋物線![]() 上一點
上一點![]() 到拋物線焦點
到拋物線焦點![]() 的距離.
的距離.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 的兩個交點為
的兩個交點為![]() ,
,![]() 兩點,已知圓
兩點,已知圓![]() :
:![]() 與
與![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() (點
(點![]() 在
在![]() 軸的正半軸),且直線
軸的正半軸),且直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 的面積與
的面積與![]() 的面積乘積的最大值.
的面積乘積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com