
【題目】某投資公司對以下兩個項目進行前期市場調研:項目![]() :通信設備.根據調研,投資到該項目上,所有可能結果為:獲利
:通信設備.根據調研,投資到該項目上,所有可能結果為:獲利![]() 、損失
、損失![]() 、不賠不賺,且這三種情況發生的概率分別為
、不賠不賺,且這三種情況發生的概率分別為![]() ;項目
;項目![]() :新能源汽車.根據調研,投資到該項目上,所有可能結果為:獲利
:新能源汽車.根據調研,投資到該項目上,所有可能結果為:獲利![]() 、虧損
、虧損![]() ,且這兩種情況發生的概率分別為
,且這兩種情況發生的概率分別為![]() .經測算,當投入
.經測算,當投入![]() 兩個項目的資金相等時,它們所獲得的平均收益(即數學期望)也相等.
兩個項目的資金相等時,它們所獲得的平均收益(即數學期望)也相等.
(1)求![]() 的值;
的值;
(2)若將![]() 萬元全部投到其中的一個項目,請你從投資回報穩定性考慮,為投資公司選擇一個合理的項目,并說明理由.
萬元全部投到其中的一個項目,請你從投資回報穩定性考慮,為投資公司選擇一個合理的項目,并說明理由.
科目:高中數學 來源: 題型:
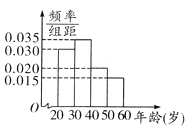
【題目】某工廠有120名工人,其年齡都在20~ 60歲之間,各年齡段人數按[20,30),[30,40),[40,50),[50,60]分成四組,其頻率分布直方圖如下圖所示.工廠為了開發新產品,引進了新的生產設備,要求每個工人都要參加A、B兩項培訓,培訓結束后進行結業考試。已知各年齡段兩項培訓結業考試成績優秀的人數如下表所示。假設兩項培訓是相互獨立的,結業考試也互不影響。
年齡分組 | A項培訓成績 優秀人數 | B項培訓成績 優秀人數 |
[20,30) | 27 | 16 |
[30,40) | 28 | 18 |
[40,50) | 16 | 9 |
[50,60] | 6 | 4 |
(1)若用分層抽樣法從全廠工人中抽取一個容量為40的樣本,求四個年齡段應分別抽取的人數;
(2)根據頻率分布直方圖,估計全廠工人的平均年齡;
(3)隨機從年齡段[20,30)和[40,50)中各抽取1人,設這兩人中A、B兩項培訓結業考試成績都優秀的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
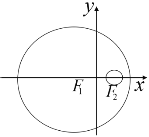
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動圓
,若動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切.
外切.
(Ⅰ)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過直線![]() 上的點
上的點![]() 作圓
作圓![]() 的兩條切線,設切點分別是
的兩條切線,設切點分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,且橢圓的短軸長為2.
,且橢圓的短軸長為2.
(1)球橢圓的標準方程;
(2)已知直線![]() 過右焦點
過右焦點![]() ,且它們的斜率乘積為
,且它們的斜率乘積為![]() ,設
,設![]() 分別與橢圓交于點
分別與橢圓交于點![]() 和
和![]() .
.
①求![]() 的值;
的值;
②設![]() 的中點
的中點![]() ,
,![]() 的中點為,求
的中點為,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題,其中正確的序號是________(寫出所有正確命題的序號).
①已知集合![]() ,
,![]() ,則映射
,則映射![]() 中滿足
中滿足![]() 的映射共有
的映射共有![]() 個;
個;
②函數![]() 的圖象關于
的圖象關于![]() 對稱的函數解析式為
對稱的函數解析式為![]() ;
;
③若函數![]() 的值域為
的值域為![]() ,則實數
,則實數![]() 的取值范圍是
的取值范圍是![]() ;
;
④已知函數![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,則
,則![]() 的值等于
的值等于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,試求函數y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)對于任意的x∈[0,2],不等式f(x)≤a成立,試求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
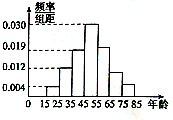
【題目】某購物中心為了了解顧客使用新推出的某購物卡的顧客的年齡分布情況,隨機調查了![]() 位到購物中心購物的顧客年齡,并整理后畫出頻率分布直方圖如圖所示,年齡落在區間
位到購物中心購物的顧客年齡,并整理后畫出頻率分布直方圖如圖所示,年齡落在區間![]() 內的頻率之比為
內的頻率之比為![]() .
.
(1) 求顧客年齡值落在區間![]() 內的頻率;
內的頻率;
(2) 擬利用分層抽樣從年齡在![]() 的顧客中選取
的顧客中選取![]() 人召開一個座談會,現從這
人召開一個座談會,現從這![]() 人中選出
人中選出![]() 人,求這兩人在不同年齡組的概率.
人,求這兩人在不同年齡組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com