
【題目】已知A={x|(2x)2﹣62x+8≤0},函數f(x)=log2x(x∈A).
(1)求函數f(x)的定義域;
(2)若函數h(x)=[f(x)]2﹣log2(2x),求函數h(x)的值域.
【答案】
(1)解:設t=2x,
∵A={x|(2x)2﹣62x+8≤0},
∴t2﹣6t+8≤0,解得2≤t≤4,
∴x∈[1,2],即函數f(x)的定義域為[1,2]
(2)解:設u=log2x,由(1)u=log2x∈[0,1],
∴ ![]() ,
,
∴h(x)∈[ ![]() ]
]
【解析】(1)設t=2x , 把(2x)2﹣62x+8≤0轉化為關于t的一元二次不等式求得t的范圍,進一步求得x的范圍得答案;(2)設u=log2x,由(1)u=log2x∈[0,1],然后利用配方法求得函數的值域.
【考點精析】通過靈活運用函數的定義域及其求法和函數的值域,掌握求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的即可以解答此題.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=ax2+bx+c(a≠0)的圖象過點(0,1)且與x軸有唯一的交點(﹣1,0).
(1)求f(x)的表達式;
(2)在(1)的條件下,設函數F(x)=f(x)﹣mx,若F(x)在區間[﹣2,2]上是單調函數,求實數m的取值范圍;
(3)設函數g(x)=f(x)﹣kx,x∈[﹣2,2],記此函數的最小值為h(k),求h(k)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種機器的固定成本為0.5萬元,但每生產1百臺時,又需可變成本(即另增加投入)0.25萬元.市場對此商品的年需求量為5百臺,銷售的收入(單位:萬元)函數為:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是產品生產的數量(單位:百臺).
x2(0≤x≤5),其中x是產品生產的數量(單位:百臺).
(1)將利潤表示為產量的函數;
(2)年產量是多少時,企業所得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 分別是雙曲線E:
分別是雙曲線E: ![]()
![]() 的左、右焦點,P是雙曲線上一點,
的左、右焦點,P是雙曲線上一點, ![]() 到左頂點的距離等于它到漸近線距離的2倍,(1)求雙曲線的漸近線方程;(2)當
到左頂點的距離等于它到漸近線距離的2倍,(1)求雙曲線的漸近線方程;(2)當![]() 時,
時, ![]() 的面積為
的面積為![]() ,求此雙曲線的方程。
,求此雙曲線的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
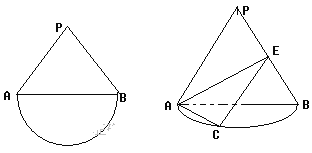
【題目】如圖是一個邊長為![]() 的正三角形和半圓組成的圖形,現把
的正三角形和半圓組成的圖形,現把![]() 沿直線AB折起使得與圓所在平面垂直,已知點C是半圓的一個三等分點(靠左邊一點),點E是線段PB上的點,(1)當點E是PB的中點時,在圓弧上找一點Q,使得
沿直線AB折起使得與圓所在平面垂直,已知點C是半圓的一個三等分點(靠左邊一點),點E是線段PB上的點,(1)當點E是PB的中點時,在圓弧上找一點Q,使得![]() 平面
平面![]() ;(2)當二面角
;(2)當二面角![]() 的正切值為
的正切值為![]() 時,求BE的長。
時,求BE的長。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農場計劃種植某種新作物,為此對這種作物的兩個品種(分別稱為品種甲和品種乙)進行田間試驗.選取兩大塊地,每大塊地分成![]() 小塊地,在總共
小塊地,在總共![]() 小塊地中,隨機選
小塊地中,隨機選![]() 小塊地種植品種甲,另外
小塊地種植品種甲,另外![]() 小塊地種植品種乙.
小塊地種植品種乙.
(1)假設![]() ,求第一大塊地都種植品種甲的概率;
,求第一大塊地都種植品種甲的概率;
(2)試驗時每大塊地分成![]() 小塊,即
小塊,即![]() ,試驗結束后得到品種甲和品種乙在各小塊地上的每公頃產量(單位:kg/hm2)如下表:
,試驗結束后得到品種甲和品種乙在各小塊地上的每公頃產量(單位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分別求品種甲和品種乙的每公頃產量的樣本平均數和樣本方差;根據試驗結果,你認為應該種植哪一品種?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F1,F2分別是橢圓E: ![]() (a>b>0)的左、右焦點,過點F1的直線交橢圓E于A,B兩點,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦點,過點F1的直線交橢圓E于A,B兩點,|AF1|=3|BF1|,若cos∠AF2B=![]() ,則橢圓E的離心率為( )
,則橢圓E的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
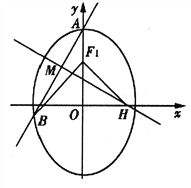
【題目】已知橢圓![]() 的上、下焦點分別為
的上、下焦點分別為![]() ,上焦點
,上焦點![]() 到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=
到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=![]() .
.
(I)求橢圓C的標準方程;
(II)設過橢圓C的上頂點A的直線![]() 與橢圓交于點B(B不在y軸上),垂直于
與橢圓交于點B(B不在y軸上),垂直于![]() 的直線與
的直線與![]() 交于點M,與
交于點M,與![]() 軸交于點H,若
軸交于點H,若![]() =0,且
=0,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com