
【題目】已知函數![]() .
.
(1)討論函數f(x)的極值點的個數;
(2)若f(x)有兩個極值點![]() ,
,![]() ,證明:
,證明:![]() .
.
【答案】(1)見解析(2)見解析
【解析】
(1)求得函數的導數![]() ,
,![]() ,按
,按![]() 、
、![]() 、
、![]() 三種情況分類討論,得出函數的單調性,進而得出函數的極值;
三種情況分類討論,得出函數的單調性,進而得出函數的極值;
(2)由(1)知,當![]() 時,
時,![]() 極值點
極值點![]() ,
,![]() 是方程
是方程![]() 的兩根,化簡得
的兩根,化簡得![]() ,設
,設![]() ,
,![]() ,利用導數求得函數
,利用導數求得函數![]() 的單調性與最值,即可求解.
的單調性與最值,即可求解.
(1)由題意,函數![]() ,
,
得![]() ,
,![]() ,
,
(i)若![]() 時;
時;![]() ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,
單調遞增,
所以當![]() ,函數
,函數![]() 取得極小值,
取得極小值,![]() 是
是![]() 的一個極小值點;
的一個極小值點;
(ii)若![]() 時,則
時,則![]() ,即
,即![]() 時,此時
時,此時![]() ,
,![]() 在
在![]() 是減函數,
是減函數,![]() 無極值點,
無極值點,
當![]() 時,則
時,則![]() ,令
,令![]() ,解得
,解得![]() ,
,![]() ,
,
當![]() 和
和![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 取得極小值,在
取得極小值,在![]() 取得極大值,所以
取得極大值,所以![]() 有兩個極值點,
有兩個極值點,
綜上可知:(i)![]() 時,
時,![]() 僅有一個極值點;(ii).當
僅有一個極值點;(ii).當![]() 時,
時,![]() 無極值點;
無極值點;
(iii)當![]() ,
,![]() 有兩個極值點.
有兩個極值點.
(2)由(1)知,當且僅當![]() 時,
時,![]() 有極小值點
有極小值點![]() 和極大值點
和極大值點![]() ,
,
且![]() ,
,![]() 是方程
是方程![]() 的兩根,∴
的兩根,∴![]() ,
,![]() ,
,
則![]()
![]()
![]()
![]()
![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,
∴![]() 時,
時,![]() 是減函數,
是減函數,![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.
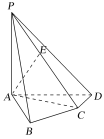
(1)求證:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小;
(3)求二面角A-PD-C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠共有![]() 名工人,已知這
名工人,已知這![]() 名工人去年完成的產品數都在區間
名工人去年完成的產品數都在區間![]() (單位:萬件)內,其中每年完成
(單位:萬件)內,其中每年完成![]() 萬件及以上的工人為優秀員工,現將其分成
萬件及以上的工人為優秀員工,現將其分成![]() 組,第
組,第![]() 組、第
組、第![]() 組、第
組、第![]() 組、第
組、第![]() 組、第
組、第![]() 組對應的區間分別為
組對應的區間分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并繪制出如圖所示的頻率分布直方圖.
,并繪制出如圖所示的頻率分布直方圖.
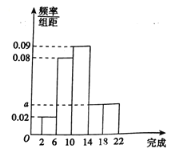
(1)求![]() 的值,并求去年優秀員工人數;
的值,并求去年優秀員工人數;
(2)選取合適的抽樣方法從這![]() 名工人中抽取容量為
名工人中抽取容量為![]() 的樣本,求這
的樣本,求這![]() 組分別應抽取的人數;
組分別應抽取的人數;
(3)現從(2)中![]() 人的樣本中的優秀員工中隨機選取
人的樣本中的優秀員工中隨機選取![]() 名傳授經驗,求選取的
名傳授經驗,求選取的![]() 名工人在同一組的概率.
名工人在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在五邊形AEBCD中,![]() ,C
,C![]() ,
,![]() ,
,![]() ,
,![]() (如圖).將△ABE沿AB折起,使平面ABE⊥平面ABCD,線段AB的中點為O(如圖).
(如圖).將△ABE沿AB折起,使平面ABE⊥平面ABCD,線段AB的中點為O(如圖).
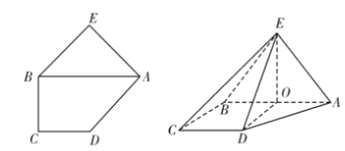
(1)求證:平面ABE⊥平面DOE;
(2)求平面EAB與平面ECD所成的銳二面角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年4月1日,新華通訊社發布:國務院決定設立河北雄安新區.消息一出,河北省雄縣、容城、安新3縣及周邊部分區域迅速成為海內外高度關注的焦點.
(1)為了響應國家號召,北京市某高校立即在所屬的8個學院的教職員工中作了“是否愿意將學校整體搬遷至雄安新區”的問卷調查,8個學院的調查人數及統計數據如下:
調查人數( | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
愿意整體搬遷人數( | 8 | 17 | 25 | 31 | 39 | 47 | 55 | 66 |
請根據上表提供的數據,用最小二乘法求出變量![]() 關于變量
關于變量![]() 的線性回歸方程
的線性回歸方程![]() 保留小數點后兩位有效數字);若該校共有教職員工2500人,請預測該校愿意將學校整體搬遷至雄安新區的人數;
保留小數點后兩位有效數字);若該校共有教職員工2500人,請預測該校愿意將學校整體搬遷至雄安新區的人數;
(2)若該校的8位院長中有5位院長愿意將學校整體搬遷至雄安新區,現該校擬在這8位院長中隨機選取4位院長組成考察團赴雄安新區進行實地考察,記![]() 為考察團中愿意將學校整體搬遷至雄安新區的院長人數,求
為考察團中愿意將學校整體搬遷至雄安新區的院長人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式及數據:  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為圓
為圓![]() 上任意一點,點
上任意一點,點![]() ,線段
,線段![]() 的中垂線交
的中垂線交![]() 于點
于點![]() .
.
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)若動直線![]() 與圓
與圓![]() 相切,且與動點
相切,且與動點![]() 的軌跡交于點
的軌跡交于點![]() 、
、![]() ,求
,求![]() 面積的最大值(
面積的最大值(![]() 為坐標原點).
為坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次調查中,甲、乙、丙、丁四位同學閱讀量有如下關系:同學甲、丙閱讀量之和與乙、丁閱讀量之和相同,同學甲、乙閱讀量之和大于丙、丁閱讀量之和,丁的閱讀量大于乙、丙閱讀量之和.那么這四名同學按閱讀量從大到小的排序依次為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com