【題目】在直角坐標系
中，已知中心在原點，離心率為
的橢圓
的一個焦點為圓
： 
的圓心．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設
是橢圓
上一點，過
作兩條斜率之積為
的直線
， 
，當直線
， 
都與圓
相切時，求
的坐標．
【答案】（1）
；（2）
．
【解析】試題分析：（1）圓心坐標是已知的，故橢圓的焦點是已知的，從而半焦距
已知了，又有離心率，故半長軸長
也能求出，從而求出
，而根據題意，橢圓方程是標準方程，可其方程易得；（2）設P點坐標為
，再設一條切線的斜率為
，則另一條切線的斜率為
，三個未知數
需要三個方程，點P在橢圓上，一個等式，兩條直線都圓的切線，利用圓心到切線的距離等于圓的半徑又得到兩個等式，三個等量關系，三個未知數理論上可解了，當然具體解題時，可設切線斜率為
，則點斜率式寫出直線方程，利用圓心到切線距離等于圓半徑得出關于
的方程，而
是這個方程的兩解，由韋達定理得
，這個結果又是
，就列出了關于P點坐標的一個方程，再由P點在橢圓上，可解出P點坐標．
試題解析：（1）圓的標準方程為
，圓心為
，所以
，又
， 
， 
，而據題意橢圓的方程是標準方程，故其方程為
．4分
（2）設
，得
∵
，依題意
到
的距離為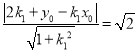
整理得
同理
∴
是方程
的兩實根10分
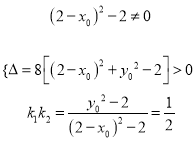12分
∴
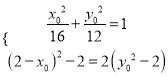14分
16分
科目：高中數學 來源： 題型：
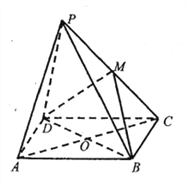
【題目】如圖，點
是菱形
所在平面外一點， 
， 
是等邊三角形， 
， 
， 
是
的中點.
（Ⅰ）求證： 
平面
；
（Ⅱ）求證：平面
平面
；
（Ⅲ）求直線
與平面
的所成角的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
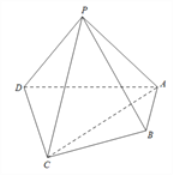
【題目】如圖，在四棱錐
中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2， 
.
（1）求證：PD⊥平面PAB；
（2）求直線PB與平面PCD所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在等腰梯形
中， 
， 
， 
，四邊形
為矩形， 
，平面
平面
，點
為線段
中點．
（Ⅰ）求異面直線
與
所成的角的正切值；
（Ⅱ）求證：平面
平面
；
（Ⅲ）求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某運動員每次投籃命中的概率為40%.現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率：先由計算器算出0到9之間取整數值的隨機數，指定1,2,3,4表示命中，5,6,7,8,9,0表示沒有命中；再以每三個隨機數為一組，代表三次投籃的結果．經隨機模擬產生了20組隨機數：
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
據此估計，該運動員三次投籃恰有兩次命中的概率為( )
A. 0.35 B. 0.25
C. 0,20 D. 0.15
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
.
（1）若橢圓
的右焦點坐標為
，求
的值；
（2）由橢圓
上不同三點構成三角形稱為橢圓的內接三角形.若以
為直角頂點的橢圓
的內接等腰直角三角形恰有三個，求
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
