
【題目】如圖,已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e= ![]() ,過點(0,﹣b),(a,0)的直線與原點的距離為
,過點(0,﹣b),(a,0)的直線與原點的距離為 ![]() ,M(x0 , y0)是橢圓上任一點,從原點O向圓M:(x﹣x0)2+(y﹣y0)2=2作兩條切線,分別交橢圓于點P,Q.
,M(x0 , y0)是橢圓上任一點,從原點O向圓M:(x﹣x0)2+(y﹣y0)2=2作兩條切線,分別交橢圓于點P,Q.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若記直線OP,OQ的斜率分別為k1 , k2 , 試求k1k2的值.
【答案】解:(Ⅰ)由橢圓的離心率e= ![]() =
= ![]() =
= ![]() ,
,
即a2=2b2 , ①
設過點(0,﹣b),(a,0)的直線方程為 ![]() ,
,
即bx﹣ay﹣ab=0,
因為直線與原點的距離為 ![]() ,
,
∴ ![]() =
= ![]() ,整理得:
,整理得: ![]() =2,②
=2,②
由①②得 ![]() ,
,
∴橢圓的方程為 ![]() ;
;
(Ⅱ)由直線OP:y=k1x,OQ:y=k2x,與圓M相切,
由直線和圓相切的條件:d=r,可得 ![]() =
= ![]() =
= ![]() ,
,
平方整理,可得k12(2﹣x02)+2k1x0y0+2﹣y02=0,
k22(2﹣x02)+2k2x0y0+2﹣y02=0,
∴k1 , k2是方程k2(2﹣x02)+2kx0y0+2﹣y02=0的兩個不相等的實數根,
k1k2= ![]() ,
,
由點R(x0 , y0)在橢圓C上,
∴ ![]() ,即y02=3(1﹣
,即y02=3(1﹣ ![]() )=3﹣
)=3﹣ ![]() x02 ,
x02 ,
∴k1k2= ![]() =﹣
=﹣ ![]() ,
,
k1k2的值為﹣ ![]() .
.
【解析】(Ⅰ)由橢圓的離心率公式可知a2=2b2 , 利用點到直線的距離公式 ![]() =2,即可求得a和b的值,即可求得橢圓方程;(Ⅱ)利用點到直線的距離公式,可知k1 , k2是方程k2(2﹣x02)+2kx0y0+2﹣y02=0的兩個不相等的實數根,利用韋達定理即可求得k1k2 , 由R(x0 , y0)在橢圓C上,y02=3﹣
=2,即可求得a和b的值,即可求得橢圓方程;(Ⅱ)利用點到直線的距離公式,可知k1 , k2是方程k2(2﹣x02)+2kx0y0+2﹣y02=0的兩個不相等的實數根,利用韋達定理即可求得k1k2 , 由R(x0 , y0)在橢圓C上,y02=3﹣ ![]() x02 , 代入即可求得k1k2的值.
x02 , 代入即可求得k1k2的值.


 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:
【題目】設函數f(x)= 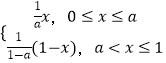 ,a為常數,且a∈(0,1).
,a為常數,且a∈(0,1).
(1)若x0滿足f(x0)=x0 , 則稱x0為f(x)的一階周期點,證明函數f(x)有且只有兩個一階周期點;
(2)若x0滿足f(f(x0))=x0 , 且f(x0)≠x0 , 則稱x0為f(x)的二階周期點,當a= ![]() 時,求函數f(x)的二階周期點.
時,求函數f(x)的二階周期點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈(0, ![]() ))的圖象在y軸上的截距為1,在相鄰兩個最值點
))的圖象在y軸上的截距為1,在相鄰兩個最值點 ![]() 和(x0 , ﹣2)上(x0>0),函數f(x)分別取最大值和最小值.
和(x0 , ﹣2)上(x0>0),函數f(x)分別取最大值和最小值.
(1)求函數f(x)的解析式;
(2)若f(x)= ![]() 在區間
在區間 ![]() 內有兩個不同的零點,求k的取值范圍;
內有兩個不同的零點,求k的取值范圍;
(3)求函數f(x)在區間 ![]() 上的對稱軸方程.
上的對稱軸方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=asinx﹣bcosx(a、b為常數,a≠0,x∈R)在x= ![]() 處取得最小值,則函數y=f(
處取得最小值,則函數y=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函數且它的圖象關于點(π,0)對稱
B.偶函數且它的圖象關于點 ![]() 對稱
對稱
C.奇函數且它的圖象關于點 ![]() 對稱
對稱
D.奇函數且它的圖象關于點(π,0)對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2alnx.
(1)若函數f(x)的圖象在(2,f(2))處的切線斜率為1,求實數a的值;
(2)求函數f(x)的單調區間;
(3)若函數 ![]() 在[1,2]上是減函數,求實數a的取值范圍.
在[1,2]上是減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C的對邊分別為a,b,c,且2asinB﹣ ![]() bcosA=0.
bcosA=0.
(1)求cosA;
(2)若a= ![]() ,b=2,求△ABC的面積.
,b=2,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com