
【題目】已知函數![]() .
.
(1)若函數![]() 與
與![]() 的圖象恰好相切與點
的圖象恰好相切與點![]() ,求實數
,求實數![]() 的值;
的值;
(2)當![]() 時,
時, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)求證: ![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
【解析】試題分析:(1)根據導數幾何意義得![]() ,即得實數
,即得實數![]() 的值;(2)利用分參法將不等式恒成立問題轉化為對應函數最值問題
的值;(2)利用分參法將不等式恒成立問題轉化為對應函數最值問題![]() (x>1)最大值,再利用導數研究函數
(x>1)最大值,再利用導數研究函數![]() 單調性:單調遞減,最后根據洛必達法則求最大值,即得實數
單調性:單調遞減,最后根據洛必達法則求最大值,即得實數![]() 的取值范圍(3)先根據和的關系轉化為對應項的關系:
的取值范圍(3)先根據和的關系轉化為對應項的關系: ![]() ,再利用(2)的結論
,再利用(2)的結論![]() ,令
,令![]() ,則代入放縮得證
,則代入放縮得證
試題解析:(1)![]()
所以![]()
(2)方法一:(分參)
即![]() 時,
時, ![]() ,
, ![]() 時,顯然成立;
時,顯然成立;
![]() 時,即
時,即![]()
令![]() ,則
,則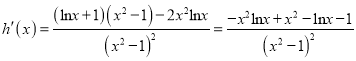
令![]() []
[]
![]()
![]() 即
即![]()
![]() 在
在![]() 上單調遞減
上單調遞減
![]()
故![]()
方法二:(先找必要條件)
注意到![]() 時,恰有
時,恰有![]()
令![]()
則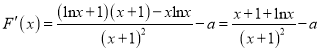
![]() 在
在![]() 恒成立的必要條件為
恒成立的必要條件為![]()
即![]()
下面證明:當![]() 時,
時, ![]()
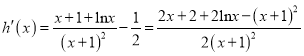
令![]()
![]() 即
即![]()
![]() 在
在![]() 遞減,
遞減,
![]() 恒成立,即
恒成立,即![]() 也是充分條件,故有
也是充分條件,故有![]() .
.
(3)不妨設![]() 為
為![]() 前
前![]() 項和,則
項和,則![]()
要證原不等式,只需證![]()
而由(2)知:當![]() 時恒有
時恒有![]()
即![]() 當且僅當
當且僅當![]() 時取等號
時取等號
取![]() ,則
,則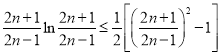
即![]() 即
即![]()
即![]() 成立,從而原不等式獲證.
成立,從而原不等式獲證.


科目:高中數學 來源: 題型:
【題目】某工廠某種產品的年固定成本為250萬元,每生產x千件,需另投入成本為C(x),當年產量不足80千件時,C(x)= ![]() (萬元).當年產量不小于80千件時,C(x)=51x+
(萬元).當年產量不小于80千件時,C(x)=51x+ ![]() (萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤L(x)(萬元)關于年產量x(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}滿足a1= ![]() ,an+1﹣an+anan+1=0(n∈N*).
,an+1﹣an+anan+1=0(n∈N*).
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)求證:a1+a1a2+a1a2a3+…+a1a2…an<1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科研小組研究發現:一棵水果樹的產量![]() (單位:百千克)與肥料費用(單位:百元)滿足如下關系:
(單位:百千克)與肥料費用(單位:百元)滿足如下關系:  .此外,還需要投入其它成本(如施肥的人工費等)
.此外,還需要投入其它成本(如施肥的人工費等)![]() 百元.已知這種水果的市場售價為16元/千克(即16百元/百千克),且市場需求始終供不應求.記該棵水果樹獲得的利潤為
百元.已知這種水果的市場售價為16元/千克(即16百元/百千克),且市場需求始終供不應求.記該棵水果樹獲得的利潤為![]() (單位:百元).
(單位:百元).
(1)求![]() 的函數關系式;
的函數關系式;
當投入的肥料費用為多少時,該水果樹獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是等差數列,下列結論中正確的是( )
A.若a1+a2>0,則a2+a3>0
B.若a1+a2<0,則a2+a3<0
C.若0<a1<a2 , 則a2> ![]()
D.若a1<0,則(a2﹣a1)(a2﹣a3)<0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e= ![]() ,過點(0,﹣b),(a,0)的直線與原點的距離為
,過點(0,﹣b),(a,0)的直線與原點的距離為 ![]() ,M(x0 , y0)是橢圓上任一點,從原點O向圓M:(x﹣x0)2+(y﹣y0)2=2作兩條切線,分別交橢圓于點P,Q.
,M(x0 , y0)是橢圓上任一點,從原點O向圓M:(x﹣x0)2+(y﹣y0)2=2作兩條切線,分別交橢圓于點P,Q.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若記直線OP,OQ的斜率分別為k1 , k2 , 試求k1k2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計算下列幾個式子,結果為 ![]() 的序號是 ①tan25°+tan35°
的序號是 ①tan25°+tan35° ![]() tan25°tan35°,
tan25°tan35°,
② ![]() ,
,
③2(sin35°cos25°+sin55°cos65°),
④ ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com