
【題目】知函數![]() (
(![]() 、
、![]() 為常數),曲線
為常數),曲線![]() 在點
在點![]() 處的切線方程是
處的切線方程是![]() .
.
(1)求![]() 、
、![]() 的值
的值
(2)求![]() 的最大值
的最大值
(3)設![]() ,證明:對任意
,證明:對任意![]() ,都有
,都有![]() .
.
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩神坐標系中的長度單位相同.已知曲線
軸的正半軸,兩神坐標系中的長度單位相同.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在曲線![]() 上求一點,使它到直線
上求一點,使它到直線![]() :
:  (
(![]() 為參數)的距離最短,寫出
為參數)的距離最短,寫出![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別是
的左右焦點分別是![]() ,橢圓C的上頂點到直線
,橢圓C的上頂點到直線![]() 的距離為
的距離為![]() ,過
,過![]() 且垂直于x軸的直線與橢圓C相交于M,N兩點,
且垂直于x軸的直線與橢圓C相交于M,N兩點,
且|MN|=1。
(I)求橢圓![]() 的方程;
的方程;
(II)過點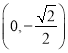 的直線與橢圓C相交于P,Q兩點,點
的直線與橢圓C相交于P,Q兩點,點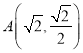 ),且
),且![]() ,求直線
,求直線![]() 的方程。
的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是定義在
是定義在![]() 上且滿足如下條件的函數
上且滿足如下條件的函數![]() 組成的集合:①對任意的
組成的集合:①對任意的![]() ,都有
,都有![]() ②存在常數
②存在常數![]() 使得對任意的
使得對任意的![]() ,都有
,都有![]() .
.
(1)設![]() 問
問![]() 是否屬于
是否屬于![]() ?說明理由;
?說明理由;
(2)若![]() 如果存在
如果存在![]() 使得
使得![]() 證明:這樣的
證明:這樣的![]() 是唯一的;
是唯一的;
(3)設![]() 且
且![]() 試求
試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x2+alnx.
x2+alnx.
(1)若a=﹣1,求函數f(x)的極值,并指出極大值還是極小值;
(2)若a=1,求函數f(x)在[1,e]上的最值;
(3)若a=1,求證:在區間[1,+∞)上,函數f(x)的圖象在g(x)=![]() x3的圖象下方.
x3的圖象下方.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy 中,曲線C1的參數方程為:![]() (
(![]() ),M是
),M是![]() 上的動點,P點滿足
上的動點,P點滿足![]() ,P點的軌跡為曲線.
,P點的軌跡為曲線.![]()
(1)求![]() 的參數方程;
的參數方程;
(2)在以O為極點,x 軸的正半軸為極軸的極坐標系中,射線![]() 與
與![]() 的異于極點的交點為A,與
的異于極點的交點為A,與![]() 的異于極點的交點為B,求
的異于極點的交點為B,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
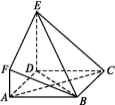
(1)求二面角F-BE-D的余弦值;
(2)設點M是線段BD上一個動點,試確定點M的位置,使得AM∥平面BEF,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構對某校高二文科學生的記憶力x和判斷力y進行統計分析,得下表數據.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
參考公式: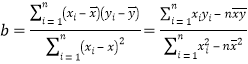
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為研究某種圖書每冊的成本費![]() (元)與印刷數
(元)與印刷數![]() (千冊)的關系,收集了一些數據并作了初步處理,得到了下面的散點圖及一些統計量的值.
(千冊)的關系,收集了一些數據并作了初步處理,得到了下面的散點圖及一些統計量的值.

|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根據散點圖判斷: ![]() 與
與![]() 哪一個更適宜作為每冊成本費
哪一個更適宜作為每冊成本費![]() (元)與印刷數
(元)與印刷數![]() (千冊)的回歸方程類型?(只要求給出判斷,不必說明理由)
(千冊)的回歸方程類型?(只要求給出判斷,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程(回歸系數的結果精確到0.01);
的回歸方程(回歸系數的結果精確到0.01);
(3)若每冊書定價為10元,則至少應該印刷多少冊才能使銷售利潤不低于78840元?(假設能夠全部售出,結果精確到1)
(附:對于一組數據![]() ,
, ![]() ,…,
,…, ![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com