
【題目】已知函數(shù)![]() ,在區(qū)間
,在區(qū)間![]() 內(nèi)任取兩個實數(shù)
內(nèi)任取兩個實數(shù)![]() ,
,![]() ,且
,且![]() ,若不等式
,若不等式![]() 恒成立,則實數(shù)
恒成立,則實數(shù)![]() 的取值范圍是
的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
分析:首先,由![]() 的幾何意義,得到直線的斜率,然后,得到函數(shù)圖象上在區(qū)間(1,2)內(nèi)任意兩點連線的斜率大于1,從而得到f′(x)=
的幾何意義,得到直線的斜率,然后,得到函數(shù)圖象上在區(qū)間(1,2)內(nèi)任意兩點連線的斜率大于1,從而得到f′(x)=![]() >1 在(1,2)內(nèi)恒成立.分離參數(shù)后,轉(zhuǎn)化成 a>2x2+3x+1在(1,2)內(nèi)恒成立.從而求解得到a的取值范圍.
>1 在(1,2)內(nèi)恒成立.分離參數(shù)后,轉(zhuǎn)化成 a>2x2+3x+1在(1,2)內(nèi)恒成立.從而求解得到a的取值范圍.
詳解:∵![]() 的幾何意義為:
的幾何意義為:
表示點(p+1,f(p+1)) 與點(q+1,f(q+1))連線的斜率,
∵實數(shù)p,q在區(qū)間(0,1)內(nèi),故p+1 和q+1在區(qū)間(1,2)內(nèi).
不等式![]() >1恒成立,
>1恒成立,
∴函數(shù)圖象上在區(qū)間(1,2)內(nèi)任意兩點連線的斜率大于1,
故函數(shù)的導(dǎo)數(shù)大于1在(1,2)內(nèi)恒成立.
由函數(shù)的定義域知,x>﹣1,
∴f′(x)=![]() >1 在(1,2)內(nèi)恒成立.
>1 在(1,2)內(nèi)恒成立.
即 a>2x2+3x+1在(1,2)內(nèi)恒成立.
由于二次函數(shù)y=2x2+3x+1在[1,2]上是單調(diào)增函數(shù),
故 x=2時,y=2x2+3x+1在[1,2]上取最大值為15,
∴a≥15
∴a∈[15,+∞).
故選:A.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學(xué)業(yè)考試導(dǎo)與練系列答案
初中學(xué)業(yè)考試導(dǎo)與練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知圓
中,已知圓![]() ,圓
,圓![]() .
.
(1)若過點![]() 的直線
的直線![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設(shè)動圓![]() 同時平分圓
同時平分圓![]() 的周長、圓
的周長、圓![]() 的周長.
的周長.
①證明:動圓圓心![]() 在一條定直線上運動;
在一條定直線上運動;
②動圓![]() 是否經(jīng)過定點?若經(jīng)過,求出定點的坐標(biāo);若不經(jīng)過,請說明理由.
是否經(jīng)過定點?若經(jīng)過,求出定點的坐標(biāo);若不經(jīng)過,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】假設(shè)某士兵遠(yuǎn)程射擊一個易爆目標(biāo),射擊一次擊中目標(biāo)的概率為![]() ,三次射中目標(biāo)或連續(xù)兩次射中目標(biāo),該目標(biāo)爆炸,停止射擊,否則就一直獨立地射擊至子彈用完.現(xiàn)有5發(fā)子彈,設(shè)耗用子彈數(shù)為隨機變量X.
,三次射中目標(biāo)或連續(xù)兩次射中目標(biāo),該目標(biāo)爆炸,停止射擊,否則就一直獨立地射擊至子彈用完.現(xiàn)有5發(fā)子彈,設(shè)耗用子彈數(shù)為隨機變量X.
(1)若該士兵射擊兩次,求至少射中一次目標(biāo)的概率;
(2)求隨機變量X的概率分布與數(shù)學(xué)期望E(X).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知表1是某年部分日期的天安門廣場升旗時刻表.
表1:某年部分日期的天安門廣場升旗時刻表

將表1中的升旗時刻化為分?jǐn)?shù)后作為樣本數(shù)據(jù)(如:![]() 可化為
可化為![]() ).
).
(Ⅰ)請補充完成下面的頻率分布表及頻率分布直方圖;
|
|
(Ⅱ)若甲學(xué)校從上表日期中隨機選擇一天觀看升旗.試估計甲學(xué)校觀看升旗的時刻早于6:00的概率;
(Ⅲ)若甲,乙兩個學(xué)校各自從表1中五月、六月的日期中隨機選擇一天觀看升旗, 求兩校觀看升旗的時刻均不早于5:00的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面幾何中,通常將完全覆蓋某平面圖形且直徑最小的圓,稱為該平面圖形的最小覆蓋圓.最小覆蓋圓滿足以下性質(zhì):①線段![]() 的最小覆蓋圓就是以
的最小覆蓋圓就是以![]() 為直徑的圓;②銳角
為直徑的圓;②銳角![]() 的最小覆蓋圓就是其外接圓.已知曲線
的最小覆蓋圓就是其外接圓.已知曲線![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為曲線
為曲線![]() 上不同的四點.
上不同的四點.
(Ⅰ)求實數(shù)![]() 的值及
的值及![]() 的最小覆蓋圓的方程;
的最小覆蓋圓的方程;
(Ⅱ)求四邊形![]() 的最小覆蓋圓的方程;
的最小覆蓋圓的方程;
(Ⅲ)求曲線![]() 的最小覆蓋圓的方程.
的最小覆蓋圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知邊長為![]() 的正
的正![]() 的頂點
的頂點![]() 在平面
在平面![]() 內(nèi),頂點
內(nèi),頂點![]() ,
,![]() 在平面
在平面![]() 外的同一側(cè),點
外的同一側(cè),點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 在平面
在平面![]() 內(nèi)的投影,設(shè)
內(nèi)的投影,設(shè)![]() ,直線
,直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .若
.若![]() 是以角
是以角![]() 為直角的直角三角形,則
為直角的直角三角形,則![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四面體ABCD中,若AB=CD= ![]() ,AC=BD=2,AD=BC=
,AC=BD=2,AD=BC= ![]() ,則直線AB與CD所成角的余弦值為( )
,則直線AB與CD所成角的余弦值為( )
A.﹣ ![]()
B.﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知長方形ABCD如圖1中,AD= ![]() ,AB=2,E為AB中點,將△ADE沿DE折起到△PDE,所得四棱錐P﹣BCDE如圖2所示.
,AB=2,E為AB中點,將△ADE沿DE折起到△PDE,所得四棱錐P﹣BCDE如圖2所示.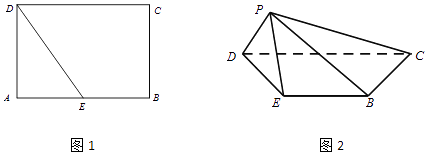
(Ⅰ)若點M為PC中點,求證:BM∥平面PDE;
(Ⅱ)當(dāng)平面PDE⊥平面BCDE時,求三棱錐E﹣PCD的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com