
【題目】若數列![]() 滿足n≥2時,
滿足n≥2時,![]() ,則稱數列
,則稱數列![]() (n
(n![]() )為
)為![]() 的“L數列”.
的“L數列”.
(1)若![]() ,且
,且![]() 的“L數列”為
的“L數列”為![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,且
,且![]() 的“L數列”為遞增數列,求k的取值范圍;
的“L數列”為遞增數列,求k的取值范圍;
(3)若![]() ,其中p>1,記
,其中p>1,記![]() 的“L數列”的前n項和為
的“L數列”的前n項和為![]() ,試判斷是否存在等差數列
,試判斷是否存在等差數列![]() ,對任意n
,對任意n![]() ,都有
,都有![]() 成立,并證明你的結論.
成立,并證明你的結論.
【答案】(1)![]() ;(2)(1,+∞);(3)存在滿足條件的等差數列
;(2)(1,+∞);(3)存在滿足條件的等差數列![]() ,見解析
,見解析
【解析】
(1)由題意知![]() 即
即![]() ,利用累乘法即可求得通項公式;(2)由
,利用累乘法即可求得通項公式;(2)由![]() 可得
可得![]() ,設
,設![]() ,根據題意{bn}為遞增數列,只需
,根據題意{bn}為遞增數列,只需![]() -
-![]() >0恒成立即可求得滿足題意的k值;(3)根據
>0恒成立即可求得滿足題意的k值;(3)根據![]() 的通項公式求出
的通項公式求出![]() ,利用放縮法及等比數列的前n項和公式可得
,利用放縮法及等比數列的前n項和公式可得![]() ,再次利用
,再次利用![]() 放縮可得
放縮可得![]() ,設
,設![]() ,易證其為等差數列,結論成立.
,易證其為等差數列,結論成立.
(1)由題意知,![]() 即
即![]() ,
,
所以![]() ,
,
即數列![]() 的通項公式為
的通項公式為![]() .
.
(2)因為![]() ,且n≥2,n∈N*時,
,且n≥2,n∈N*時,![]() ,所以
,所以![]() ,
,
設![]() ,n∈N*,所以
,n∈N*,所以![]() 1-
1-![]() .
.
因為{bn}為遞增數列,所以![]() 對n∈N*恒成立,
對n∈N*恒成立,
即![]() -
-![]() >0對
>0對![]() 恒成立.
恒成立.
因為![]() -
-![]() =
=![]() ,
,
所以![]() -
-![]() >0等價于
>0等價于![]() .
.
當0<k≤1時,因為n=1時,![]() ,不符合題意.
,不符合題意.
當k>1時,![]() ,所以
,所以![]() ,
,
綜上,k的取值范圍是![]() .
.
(3)存在滿足條件的等差數列![]() ,證明如下:
,證明如下:
因為 ,k
,k![]() ,
,
所以![]() ,又因為
,又因為![]() ,所以
,所以![]() ,
,
所以![]() ,
,
即![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
設![]() ,則
,則![]() ,且
,且![]() ,
,
所以存在等差數列![]() 滿足題意.
滿足題意.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】眾所周知的“太極圖”,其形狀如對稱的陰陽兩魚互抱在一起,也被稱為“陰陽魚太極圖”.如圖是放在平面直角坐標系中的“太極圖”.整個圖形是一個圓形.其中黑色陰影區域在y軸右側部分的邊界為一個半圓,給出以下命題:
①在太極圖中隨機取一點,此點取自黑色陰影部分的概率是![]()
②當![]() 時,直線y=ax+2a與白色部分有公共點;
時,直線y=ax+2a與白色部分有公共點;
③黑色陰影部分(包括黑白交界處)中一點(x,y),則x+y的最大值為2;
④設點P(﹣2,b),點Q在此太極圖上,使得∠OPQ=45°,b的范圍是[﹣2,2].
其中所有正確結論的序號是( )
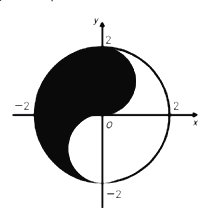
A.①④B.①③C.②④D.①②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】受突如其來的新冠疫情的影響,全國各地學校都推遲2020年的春季開學.某學校“停課不停學”,利用云課平臺提供免費線上課程.該學校為了解學生對線上課程的滿意程度,隨機抽取了500名學生對該線上課程評分.其頻率分布直方圖如下:若根據頻率分布直方圖得到的評分低于80分的概率估計值為0.45.
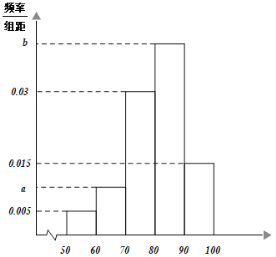
(1)(i)求直方圖中的a,b值;
(ii)若評分的平均值和眾數均不低于80分視為滿意,判斷該校學生對線上課程是否滿意?并說明理由(同一組中的數據用該組區間的中點值為代表);
(2)若采用分層抽樣的方法,從樣本評分在[60,70)和[90,100]內的學生中共抽取5人進行測試來檢驗他們的網課學習效果,再從中選取2人進行跟蹤分析,求這2人中至少一人評分在[60,70)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() .過焦點且垂直于
.過焦點且垂直于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 相交所得的弦長為3,直線
相交所得的弦長為3,直線![]() 與橢圓
與橢圓![]() 相切.
相切.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() ,問直線
,問直線![]() 是否存在?若存在,求直線
是否存在?若存在,求直線![]() 的斜率
的斜率![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P—ABCD中,底面ABCD為矩形,平面PAD⊥平面ABCD,PAPD,E,F分別為AD,PB的中點.求證:
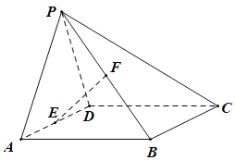
(1)EF//平面PCD;
(2)平面PAB平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的五面體中,平面
為頂點的五面體中,平面![]() 平面
平面![]() ,
,![]() ,四邊形
,四邊形![]() 為平行四邊形,且
為平行四邊形,且![]() .
.

(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為60°,求平面
所成角為60°,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學計劃用他姓名的首字母![]() ,身份證的后4位數字(4位數字都不同)以及3個符號
,身份證的后4位數字(4位數字都不同)以及3個符號![]() 設置一個六位的密碼.若
設置一個六位的密碼.若![]() 必選,且符號不能超過兩個,數字不能放在首位和末位,字母和數字的相對順序不變,則他可設置的密碼的種數為( )
必選,且符號不能超過兩個,數字不能放在首位和末位,字母和數字的相對順序不變,則他可設置的密碼的種數為( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程:
的參數方程: (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)過曲線![]() 上一點
上一點![]() 作直線
作直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,中點為
兩點,中點為![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國新型冠狀病毒肺炎疫情期間,以網絡購物和網上服務所代表的新興消費展現出了強大的生命力,新興消費將成為我國消費增長的新動能.某市為了了解本地居民在2020年2月至3月兩個月網絡購物消費情況,在網上隨機對1000人做了問卷調查,得如下頻數分布表:
網購消費情況(元) |
|
|
|
|
|
頻數 | 300 | 400 | 180 | 60 | 60 |
(1)作出這些數據的頻率分布直方圖,并估計本市居民此期間網絡購物的消費平均值;
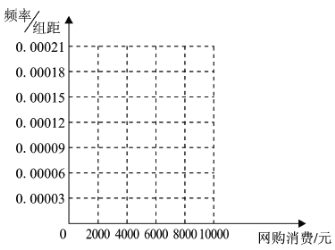
(2)在調查問卷中有一項是填寫本人年齡,為研究網購金額和網購人年齡的關系,以網購金額是否超過4000元為標準進行分層抽樣,從上述1000人中抽取200人,得到如下列聯表,請將表補充完整并根據列聯表判斷,在此期間是否有95%的把握認為網購金額與網購人年齡有關.
網購不超過4000元 | 網購超過4000元 | 總計 | |
40歲以上 | 75 | 100 | |
40歲以下(含40歲) | |||
總計 | 200 |
參考公式和數據:![]() .(其中
.(其中![]() 為樣本容量)
為樣本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com