【題目】已知過拋物線
的焦點
，斜率為
的直線交拋物線于
兩點，且
.
（1）求該拋物線
的方程；
（2）過點
任意作互相垂直的兩條直線
，分別交曲線
于點
和
.設線段
的中點分別為
，求證：直線
恒過一個定點.
【答案】（1）
（2見解析
【解析】試題分析： 
聯立直線方程和拋物線方程，利用弦長公式列方程解出
，即可得到拋物線
的方程；
設直線
的方程，聯立拋物線方程得兩根之和，計算點
的坐標，同理可得點
的坐標，運用直線點斜式給出直線方程，討論斜率問題即可得出定點
解析：（1）拋物線的焦點
，∴直線
的方程為： 
聯立方程組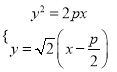
，消元得： 
，
∴
∴
，解得
.
∵
，∴拋物線
的方程為： 
.
（2）設
兩點坐標分別為
，則點
的坐標為
..
由題意可設直線
的方程為
.
由
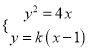，得
.
因為直線
與曲線
于
兩點，所以
.
所以點
的坐標為
.
由題知，直線
的斜率為
，同理可得點
的坐標為
.
當
時，有
，此時直線
的斜率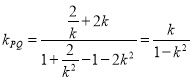
.
所以，直線
的方程為
，整理得
.
于是，直線
恒過定點
；
當
時，直線
的方程為
，也過點
.
綜上所述，直線
恒過定點
.
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案
第三學期贏在暑假系列答案科目：高中數學 來源： 題型：
【題目】已知函數
的部分圖象如圖所示，
分別是圖象的最低點和最高點，
.
（1）求函數
的解析式；
（2）將函數
的圖象向左平移
個單位長度，再把所得圖象上各點橫坐標伸長到原來的2倍（縱坐標不變），得到函數
的圖象，求函數
的單調遞增區間.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A={x2|x2+2x-3<0},B=
.
(1)在區間(-4,4)上任取一個實數x,求“x∈A∩B”的概率;
(2)設(a,b)為有序實數對,其中a是從集合A中任取的一個整數,b是從集合B中任取的一個整數,求“b-a∈A∪B”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校團委組織了“文明出行，愛我中華”的知識競賽，從參加考試的學生中抽出60名學生，將其成績（單位：分）整理后，得到如下頻率分布直方圖（其中分組區間為
，
，…，
）.
（1）求成績在
的頻率，并補全此頻率分布直方圖；
（2）求這次考試平均分的估計值；
（3）若從成績在和的學生中任選兩人，求他們的成績在同一分組區間的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在路邊安裝路燈，路寬為
，燈柱
長為
米，燈桿
長為1米，且燈桿與燈柱成
角，路燈采用圓錐形燈罩，其軸截面的頂角為
，燈罩軸線
與燈桿
垂直．
⑴設燈罩軸線與路面的交點為
，若
米，求燈柱
長；
⑵設
米，若燈罩截面的兩條母線所在直線一條恰好經過點
，另一條與地面的交點為
（如圖2）
（圖1） （圖2）
（ⅰ）求
的值；（ⅱ）求該路燈照在路面上的寬度
的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若點P是直線2x＋y＋10＝0上的動點，直線PA、PB分別與圓x2＋y2＝4相切于A、B兩點，則四邊形PAOB(O為坐標原點)面積的最小值為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合A={x|x2+2x﹣3＜0}，集合B={x||x+a|＜1}．
（1）若a=3，求A∪B；
（2）設命題p：x∈A，命題q：x∈B，若p是q成立的必要不充分條件，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
