
【題目】已知函數![]() ,
,![]() (
(![]() ).
).
(1)若![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() 對于任意的實數
對于任意的實數![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)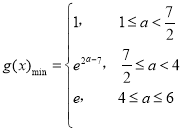 .
.
【解析】
(1)利用基本不等式求解最值;
(2)轉化為![]() 對于任意的實數x恒成立,求參數的取值范圍;
對于任意的實數x恒成立,求參數的取值范圍;
(3)函數去絕對值,等價轉化為比較![]() 與
與![]() 的大小關系,數形結合求解.
的大小關系,數形結合求解.
(1)對于![]() ,
,![]() ,
,
所以![]()
![]() ,
,
當且僅當![]() ,即
,即![]() 時等號成立,所以
時等號成立,所以![]() .
.
(2)![]() 對于任意的實數x恒成立,即
對于任意的實數x恒成立,即![]() 對于任意的實數x恒成立,亦即
對于任意的實數x恒成立,亦即![]() 對于任意的實數x恒成立,
對于任意的實數x恒成立,
所以![]() ,即
,即![]() 對于任意的實數x恒成立.
對于任意的實數x恒成立.
又![]() 對于任意的實數x恒成立,
對于任意的實數x恒成立,
故只需![]() ,解得
,解得![]() ,所以
,所以![]() 的取值范圍為
的取值范圍為![]() .
.
(3)![]()
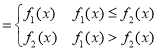 ,
,
因為![]() 與
與![]() 的底數都同為e,外函數都單調遞增,
的底數都同為e,外函數都單調遞增,
所以,比較![]() 與
與![]() 的大小關系,只須比較
的大小關系,只須比較![]() 與
與![]() 的大小關系.
的大小關系.
令![]() ,
,![]() ,
,
 ,其中
,其中![]() ,
,![]() .
.
因為![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() ,由題意可得如下圖象:
,由題意可得如下圖象:
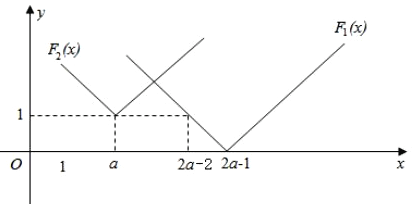
(i)當![]() ,即
,即![]() 時,
時,![]() ,
,![]() ;
;
(ii)當![]() ,即
,即![]() 時,
時,![]() ,
,![]() ;
;
(iii)當![]() ,即
,即![]() 時,
時,![]() ,
,![]() ;
;
綜上所述,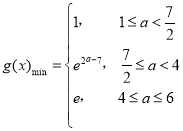 .
.


科目:高中數學 來源: 題型:
【題目】趙爽是我國古代數學家、天文學家大約在公元222年趙爽為《周碑算經》一書作序時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”(以弦為邊長得到的正方形是由4個全等的直角三角形再加上中間的一個小正方形組成的)類比“趙爽弦圖”,趙爽弦圖可類似地構造如圖所示的圖形,它是由個3全等的等邊三角形與中間的一個小等邊三角形組成的一個大等邊三角形,設DF2AF,若在大等邊三角形中隨機取一點,則此點取自小等邊三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市約有20萬住戶,為了節約能源,擬出臺“階梯電價”制度,即制定住戶月用電量的臨界值![]() ,若某住戶某月用電量不超過
,若某住戶某月用電量不超過![]() 度,則按平價(即原價)0.5(單位:元/度)計費;若某月用電量超過
度,則按平價(即原價)0.5(單位:元/度)計費;若某月用電量超過![]() 度,則超出部分按議價
度,則超出部分按議價![]() (單位:元/度)計費,未超出部分按平價計費.為確定
(單位:元/度)計費,未超出部分按平價計費.為確定![]() 的值,隨機調查了該市100戶的月用電量,統計分析后得到如圖所示的頻率分布直方圖.根據頻率分布直方圖解答以下問題(同一組數據用該區間的中點值作代表).
的值,隨機調查了該市100戶的月用電量,統計分析后得到如圖所示的頻率分布直方圖.根據頻率分布直方圖解答以下問題(同一組數據用該區間的中點值作代表).
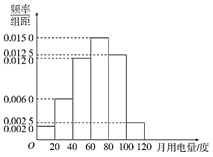
(1)若該市計劃讓全市![]() 的住戶在“階梯電價”出臺前后繳納的電費不變,求臨界值
的住戶在“階梯電價”出臺前后繳納的電費不變,求臨界值![]() ;
;
(2)在(1)的條件下,假定出臺“階梯電價”之后,月用電量未達![]() 度的住戶用電量保持不變;月用電量超過
度的住戶用電量保持不變;月用電量超過![]() 度的住戶節省“超出部分”的
度的住戶節省“超出部分”的![]() ,試估計全市每月節約的電量;
,試估計全市每月節約的電量;
(3)在(1)(2)條件下,若出臺“階梯電價”前后全市繳納電費總額不變,求議價![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
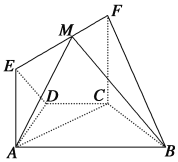
【題目】如圖,在幾何體![]() 中,
中,![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() .
.
(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上運動,設平面
上運動,設平面![]() 與平面
與平面![]() 所成二面角的平面角為
所成二面角的平面角為![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過點![]() 作圓
作圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() 、
、![]() ,給出下列四個結論:
,給出下列四個結論:
①![]() ;
;
②若![]() 為直角三角形,則
為直角三角形,則![]() ;
;
③![]() 外接圓的方程為
外接圓的方程為![]() ;
;
④直線![]() 的方程為
的方程為![]() .
.
其中所有正確結論的序號為( )
A.②④B.③④C.②③D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠采用甲、乙兩種不同生產方式生產某零件,現對兩種生產方式所生產的這種零件的產品質量進行對比,其質量按測試指標可劃分為:指標在區間![]() 100的為一等品;指標在區間
100的為一等品;指標在區間![]() 的為二等品
的為二等品![]() 現分別從甲、乙兩種不同生產方式所生產的零件中,各自隨機抽取100件作為樣本進行檢測,測試指標結果的頻率分布直方圖如圖所示:
現分別從甲、乙兩種不同生產方式所生產的零件中,各自隨機抽取100件作為樣本進行檢測,測試指標結果的頻率分布直方圖如圖所示:
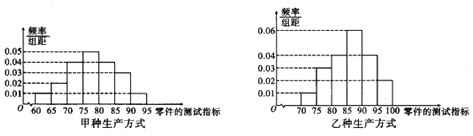
![]() 若在甲種生產方式生產的這100件零件中按等級,利用分層抽樣的方法抽取10件,再從這10件零件中隨機抽取3件,求至少有1件一等品的概率;
若在甲種生產方式生產的這100件零件中按等級,利用分層抽樣的方法抽取10件,再從這10件零件中隨機抽取3件,求至少有1件一等品的概率;
![]() 將頻率分布直方圖中的頻率視作概率,用樣本估計總體
將頻率分布直方圖中的頻率視作概率,用樣本估計總體![]() 若從該廠采用乙種生產方式所生產的所有這種零件中隨機抽取3件,記3件零件中所含一等品的件數為X,求X的分布列及數學期望.
若從該廠采用乙種生產方式所生產的所有這種零件中隨機抽取3件,記3件零件中所含一等品的件數為X,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】請解答以下問題,要求解決兩個問題的方法不同.
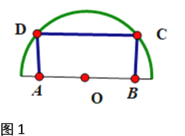
(1)如圖1,要在一個半徑為1米的半圓形鐵板中截取一塊面積最大的矩形![]() ,如何截取?并求出這個最大矩形的面積.
,如何截取?并求出這個最大矩形的面積.
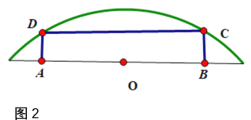
(2)如圖2,要在一個長半軸為2米,短半軸為1米的半個橢圓鐵板中截取一塊面積最大的矩形![]() ,如何截取?并求出這個最大矩形的面積.
,如何截取?并求出這個最大矩形的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com