
如圖所示,設橢圓的中心為原點O,長軸在x軸上,上頂點為A,左、右焦點分別為F1、F2,線段OF1、OF2的中點分別為B1、B2,且△AB1B2是面積為4的直角三角形.
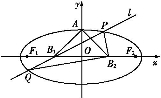
(1)求該橢圓的離心率和標準方程;
(2)過B1作直線交橢圓于P、Q兩點,使PB2⊥QB2,求△PB2Q的面積.
(1) 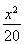 +
+ =1
=1  (2)
(2) 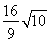
【解析】
解:(1)設橢圓的標準方程為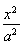 +
+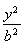 =1(a>b>0),焦距為2c,則A(0,b),|OB1|=|OB2|=
=1(a>b>0),焦距為2c,則A(0,b),|OB1|=|OB2|= .
.
由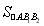 =4得
=4得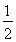 ·c·b=4,
·c·b=4,
即bc=8.①
又△AB1B2是直角三角形,
且|OB1|=|OB2|,∴b= .②
.②
由①②可得b=2,c=4.
∴a2=20.
∴橢圓的標準方程為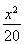 +
+ =1,離心率e=
=1,離心率e= =
= .
.
(2)由(1)知B1(-2,0),B2(2,0).
由題意知,直線PQ的傾斜角不為0,
故可設直線PQ的方程為x=my-2.
代入橢圓方程得(m2+5)y2-4my-16=0.(*)
設P1(x1,y1),P2(x2,y2),
則y1,y2是方程(*)的兩根.
∴y1+y2=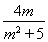 ,y1·y2=-
,y1·y2=-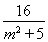 .
.
又 =(x1-2,y1),
=(x1-2,y1),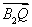 =(x2-2,y2).
=(x2-2,y2).
∴ ·
·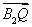 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2
=(my1-4)(my2-4)+y1y2
=(m2+1)y1y2-4m(y1+y2)+16
=-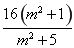 -
- +16
+16
=- .
.
由PB2⊥B2Q知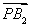 ·
·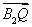 =0,
=0,
即- =0,
=0,
16m2-64=0,解得m=±2.
當m=2時,y1+y2= ,y1y2=-
,y1y2=-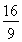 ,
,
|y1-y2|=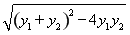 =
= .
.
 =
=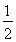 |B1B2|·|y1-y2|=
|B1B2|·|y1-y2|=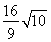 .
.
當m=-2時,由橢圓的對稱性可得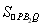 =
=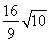 .
.
綜上所述,△PB2Q的面積為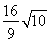 .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數學 來源: 題型:
 如圖所示,在邊長為a的正方形組成的網格中,設橢圓C1、C2、C3的離心率分別為e1、e2、e3,則e1、e2、e3的關系為
如圖所示,在邊長為a的正方形組成的網格中,設橢圓C1、C2、C3的離心率分別為e1、e2、e3,則e1、e2、e3的關系為查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,設橢圓
如圖所示,設橢圓| x2 |
| a2 |
| y2 |
| b2 |
A、 |
B、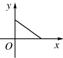 |
C、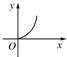 |
D、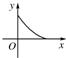 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
 如圖所示,設橢圓
如圖所示,設橢圓 +
+ =1(a>b>0)的面積為abπ,過坐標原點的直線l、x軸正半軸及橢圓圍成兩區域面積分別設為s、t,則s關于t的函數圖象大致形狀為圖中的
=1(a>b>0)的面積為abπ,過坐標原點的直線l、x軸正半軸及橢圓圍成兩區域面積分別設為s、t,則s關于t的函數圖象大致形狀為圖中的



查看答案和解析>>
科目:高中數學 來源:2013年高考數學復習卷B(七)(解析版) 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:
如圖所示,設橢圓![]() +
+![]() =1(a>b>0)的面積為abπ,過坐標原點的直線l、x軸正半軸及橢圓圍成兩區域面積分別設為s、t,則s關于t的函數圖象大致形狀為圖中的
=1(a>b>0)的面積為abπ,過坐標原點的直線l、x軸正半軸及橢圓圍成兩區域面積分別設為s、t,則s關于t的函數圖象大致形狀為圖中的
 ( )
( )
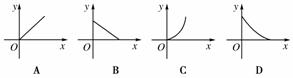
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com