
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,正項等比數列
,正項等比數列![]() 中,
中,![]() ,
,![]() ,則
,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
數列{an}的前n項和Sn=n2﹣n,a1=S1=0,n≥2時,an=Sn﹣Sn﹣1,可得an.設正項等比數列
{bn}的公比為q>0,b2=a3=4.bn+3bn﹣1=4bn2(n≥2,n∈N+),化為q2=4,解得q,可得bn.
數列{an}的前n項和Sn=n2﹣n,
∴a1=S1=0,n≥2時,an=Sn﹣Sn﹣1=2n﹣2,n=1時也成立.
∴an=2n﹣2.
設正項等比數列{bn}的公比為q>0,b2=a3=4.
bn+3bn﹣1=4bn2(n≥2,n∈N+),
∴![]() =4
=4![]() ,化為q2=4,解得q=2.
,化為q2=4,解得q=2.
∴b1×2=4,解得b1=2.
∴bn=2n.
則log2bn=n.
故答案為:D


科目:高中數學 來源: 題型:
【題目】如圖,摩天輪的半徑為40米,摩天輪的軸O點距離地面的高度為45米,摩天輪勻速逆時針旋轉,每6分鐘轉一圈,摩天輪上點P的起始位置在最高點處,下面的有關結論正確的有( )

A.經過3分鐘,點P首次到達最低點
B.第4分鐘和第8分鐘點P距離地面一樣高
C.從第7分鐘至第10分鐘摩天輪上的點P距離地面的高度一直在降低
D.摩天輪在旋轉一周的過程中有2分鐘距離地面不低于65米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在著名的漢諾塔問題中,有三根高度相同的柱子和一些大小及顏色各不相同的圓盤,三根柱子分別為起始柱、輔助柱及目標柱.已知起始柱上套有![]() 個圓盤,較大的圓盤都在較小的圓盤下面.現把圓盤從起始柱全部移到目標柱上,規則如下:每次只能移動一個圓盤,且每次移動后,每根柱上較大的圓盤不能放在較小的圓盤上面,規定一個圓盤從任一根柱上移動到另一根柱上為一次移動.若將
個圓盤,較大的圓盤都在較小的圓盤下面.現把圓盤從起始柱全部移到目標柱上,規則如下:每次只能移動一個圓盤,且每次移動后,每根柱上較大的圓盤不能放在較小的圓盤上面,規定一個圓盤從任一根柱上移動到另一根柱上為一次移動.若將![]() 個圓盤從起始柱移動到目標柱上最少需要移動的次數記為
個圓盤從起始柱移動到目標柱上最少需要移動的次數記為![]() ,則
,則![]() __________,
__________,![]() __________.
__________.
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數fn(x)=xn+bx+c(n∈Z,b,c∈R).
(1)若n=﹣1,且f﹣1(1)=f﹣1(![]() )=5,試求實數b,c的值;
)=5,試求實數b,c的值;
(2)設n=2,若對任意x1,x2∈[﹣1,1]有|f2(x1)﹣f2(x2)|≤6恒成立,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學高三文科班學生共有800人參加了數學與地理的水平測試,學校決定利用隨機數表法從中抽取100人進行成績抽樣調查,先將800人按001,002,…,800進行編號.
(1)如果從第8行第7列的數開始向右讀,請你依次寫出最先檢查的3個人的編號;
(下面摘取了第7行到第9行)

(2)抽取的100人的數學與地理的水平測試成績如下表:成績分為優秀、良好、及格三個等級;橫向,縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有![]() .
.
①若在該樣本中,數學成績優秀率是![]() ,求
,求![]() 的值:
的值:
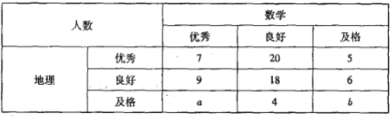
②在地理成績及格的學生中,已知![]() ,求數學成績優秀的人數比及格的人數少的概率.
,求數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調區間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,-2),橢圓E: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,F是橢圓E的右焦點,直線AF的斜率為
,F是橢圓E的右焦點,直線AF的斜率為![]() ,O為坐標原點.
,O為坐標原點.
(1)求E的方程;
(2)設過點A的動直線l與E相交于P,Q兩點.當△OPQ的面積最大時,求l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的最大值;
的最大值;
(2)令![]() ,
,![]() 其圖象上任意一點
其圖象上任意一點![]() 處切線的斜率
處切線的斜率![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
,![]() ,方程
,方程![]() 有唯一實數解,求正數
有唯一實數解,求正數![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com