
、已知向量 =(1,2),
=(1,2),  =(-2,1),k,t為正實數(shù),向量
=(-2,1),k,t為正實數(shù),向量  =
=  +(t
+(t +1)
+1) ,
,
 =-k
=-k +
+

(1)若 ⊥
⊥ ,求k的最小值;
,求k的最小值;
(2)是否存在正實數(shù)k、t,使 ∥
∥ ? 若存在,求出k的取值范圍;若不存在,請說明理由.
? 若存在,求出k的取值范圍;若不存在,請說明理由.
(1)x=a+(t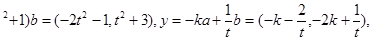
由x⊥y,得x·y=0,即(-2t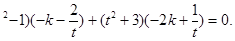
整理得k=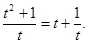 ∵t>0,∴k=
∵t>0,∴k=
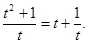 ≥2
≥2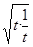 =2,當(dāng)且僅當(dāng)t=1時,k=2.
=2,當(dāng)且僅當(dāng)t=1時,k=2.
所以k的最小值為2.
(2)假設(shè)存在正實數(shù)k,t使x∥y,則(-2t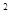 -1)(-2k+
-1)(-2k+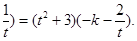 整理得tk(t
整理得tk(t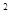 +1)+1=0.
+1)+1=0.
滿足上述等式的正實數(shù)k、t不存在,所以不存在正實數(shù)k、t,使x∥y.
【解析】(1)利用 ⊥
⊥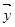 坐標(biāo)化后建立關(guān)于k的方程,然后用t表示出k,從而得到k關(guān)于t的函數(shù)關(guān)系式,再考慮采用函數(shù)求最值的方法求k的最值.
坐標(biāo)化后建立關(guān)于k的方程,然后用t表示出k,從而得到k關(guān)于t的函數(shù)關(guān)系式,再考慮采用函數(shù)求最值的方法求k的最值.
(II) 假設(shè)存在正實數(shù)k,t使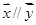 ,則(-2t
,則(-2t -1)(-2k+
-1)(-2k+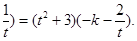 然后得到關(guān)于k,t的方程,判斷此方程是否有解即可.
然后得到關(guān)于k,t的方程,判斷此方程是否有解即可.
(1)x=a+(t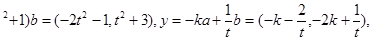
由x⊥y,得x·y=0,即(-2t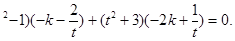
整理得k=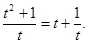 ∵t>0,∴k=
∵t>0,∴k=
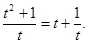 ≥2
≥2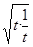 =2,當(dāng)且僅當(dāng)t=1時,k=2.
=2,當(dāng)且僅當(dāng)t=1時,k=2.
所以k的最小值為2.
(2)假設(shè)存在正實數(shù)k,t使x∥y,則(-2t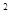 -1)(-2k+
-1)(-2k+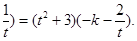 整理得tk(t
整理得tk(t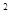 +1)+1=0.
+1)+1=0.
滿足上述等式的正實數(shù)k、t不存在,所以不存在正實數(shù)k、t,使x∥y.


 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣東省東莞市高三上學(xué)期9月月考理科數(shù)學(xué)試卷(解析版) 題型:選擇題
已知向量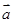 =
(1,2 ),
=
(1,2 ), 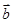 =
(2,-3 ),若向量
=
(2,-3 ),若向量 滿足(
滿足( +
+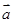 )//
)//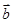 ,
, ⊥(
⊥(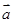 +
+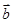 ),則
),則 =( )
=( )
A.( ,
, )
B.(-
)
B.(- ,-
,- )
)
C.( ,
, )
D.(-
)
D.(- ,-
,- )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年高考試題數(shù)學(xué)文(重慶卷)解析版 題型:選擇題
已知向量 =(1,
=(1, ) ,
) , =(2,2)
,且
=(2,2)
,且 與
與 共線,那么
共線,那么 的值為
的值為
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com