Question

【題目】從某居民區隨機抽取10個家庭，獲得第i個家庭的月收入xi（單位：千元）與月儲蓄yi（單位：千元）的數據資料，算得 ， ， ， ．
（Ⅰ）求家庭的月儲蓄y對月收入x的線性回歸方程y=bx+a；
（Ⅱ）判斷變量x與y之間是正相關還是負相關；
（Ⅲ）若該居民區某家庭月收入為7千元，預測該家庭的月儲蓄．
附：線性回歸方程y=bx+a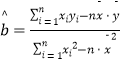中， ， ，其中 ， 為樣本平均值，線性回歸方程也可寫為 ．

Answer 1

【答案】解：（Ⅰ）由題意可知n=10， = = =8， = = =2，故lxx= =720﹣10×82=80，lxy= =184﹣10×8×2=24，
故可得b= ═ =0.3，a= =2﹣0.3×8=﹣0.4，
故所求的回歸方程為：y=0.3x﹣0.4；
（Ⅱ）由（Ⅰ）可知b=0.3＞0，即變量y隨x的增加而增加，故x與y之間是正相關；
（Ⅲ）把x=7代入回歸方程可預測該家庭的月儲蓄為y=0.3×7﹣0.4=1.7（千元）
【解析】（Ⅰ）由題意可知n， ， ，進而可得 ， ，代入可得b值，進而可得a值，可得方程；（Ⅱ）由回歸方程x的系數b的正負可判；（Ⅲ）把x=7代入回歸方程求其函數值即可．